第一步：判断题型------本题为几何问题

第二步：分析作答
设三角形S1、S2、S3的边长为a、b、b（S2=S3，所以这两个正方形的边长相等），中间两个面积为3、2的正方形的边长分别为c、d，如下图所示：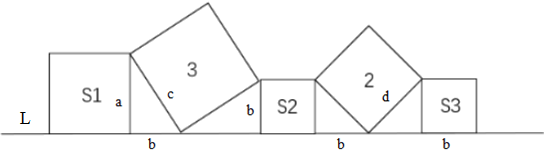

由于S1和S2中间夹着的两个直角三角形全等（角相等，斜边相等），S2和S3同理；
则由勾股定理得：a²+b²=c²=3，b²+b²=d²=2；
则b²=1，a²=2；
故S1+S2+S3=a²+b²+c²=2+1+1=4。

故本题选A。
【2020-四川下-049】