(单选试题)
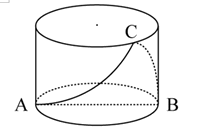
一个不计厚度的圆柱型无盖透明塑料桶,桶高2.5分米,底面周长为24分米,AB为底面直径。在塑料桶内壁桶底的B处有一只蚊子,此时,一只壁虎正好在塑料桶外壁的A处,则壁虎从外壁A处爬到内壁B处吃到蚊子所爬过的最短路径长约为:
A、
10分米
B、
12.25分米
C、
12.64分米
D、
13分米
正确答案:C,正确率:29%,作答次数:2528
能看懂解析
看不懂解析
收藏
纠错
答案解析
第一步:判断题型-------本题为几何问题
第二步:题目详解
从外壁走到内壁,最短情况有两种可能,分别为:
(一)圆柱侧面不展开:
根据两点之间直线最短,壁虎从A点沿着外壁直上直下爬入桶内部走了2.5+2.5=5,由于不计筒壁厚度,此时壁虎相当于在内壁的A点处,然后再走直径即可到达桶内壁的B处,走了直径=24÷π≈24÷3.14≈7.64,此时的最短距离=5+7.64=12.64分米。
(二)圆柱侧面展开为矩形:
根据直线同侧两点到直线上同一点距离之和最短用对称点法,画出A点的对称A′,即可将A、B两点放在同一个平面上并连线,如下图所示: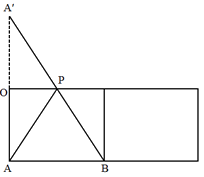
在直角三角形AA′B中,根据勾股定理:A′A²+AB²+=A′B²。
A′A =2.5×2=5,AB=12,则![]() ,即最短距离为13分米。
,即最短距离为13分米。
综上,(一)这种最短,爬过的最短路径长约为12.64分米。
故本题选C。
【2021-联考/山西-069】
视频解析

评分:
还没有人评价哦,试试发表评价吧
评价列表
发表评价

来源
 陕公网安备 61010302000399号
陕公网安备 61010302000399号