(单选试题)
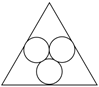
某市江滨有一处边长为50米的等边三角形广场。广场里设计有三个大小相等的圆环鹅卵石道路供市民散步。如下图所示,各圆相切,各圆与三角形也相切。问沿三个圆环外围石道(不含圆切点之间的弧)散步一圈约为多少米?
A、
95
B、
105
C、
115
D、
125
正确答案:B,正确率:42%,作答次数:2833
能看懂解析
看不懂解析
收藏
纠错
答案解析
第一步:判断题型------本题为几何问题
第二步:分析解题
如下图所示,连接三个内切圆的圆心,组成的依旧是等边三角形,则三个圆之间的弧心角都为60°,占整个圆心角360°的1/6,由此可知三个圆之间的弧长都占三个小圆周长的1/6,则剩余部分占三个小圆周长的1-1/6=5/6,则三个圆环外围石道(不含圆切点之间的弧)=2πr×5/6×3=5πr,求出小圆半径即可求解。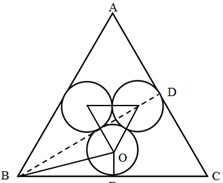
做辅助线BD垂直AC,则∠DBC=30°,从小圆圆心O引一条垂线交BC于E,连接OB,则OB平分∠DBC,故∠OBC=30°÷2=15°;
根据tan15°= OE/BE≈0.268,BE=50÷2=25,可得OE≈25× 0.268=6.7;
则三个圆环外围石道=5πr≈5×3.14×6.7≈105米。
故本题选B。
备注:![]() ;
;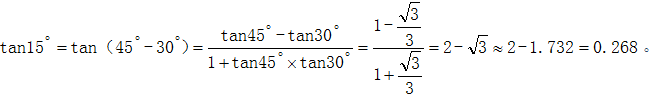
【2021-联考/山西-074】
视频解析

评分:
评价列表
发表评价

来源
 陕公网安备 61010302000399号
陕公网安备 61010302000399号