一个正八面体两个相对的顶点分别为A和B，一个点从A出发，沿八面体的棱移动到B位置，其中任何顶点最多到

（单选试题）

一个正八面体两个相对的顶点分别为A和B，一个点从A出发，沿八面体的棱移动到B位置，其中任何顶点最多到达1次，且全程必须走过所有8个面的至少1条边，问有多少种不同的走法：

A、

B、

C、

D、

正确答案：A，正确率：14%，作答次数：286

能看懂解析

看不懂解析

纠错

答案解析

第一步：判断题型------本题为几何问题

第二步：分析解题：
如下图所示：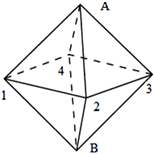
xiaomai
要想从A到B，需要先经过中间平面上的四个点1、2、3、4，最后再到达B点。假设先到1，则有1-2-3-4-B和1-4-3-2-B两条路径；
同理，先到其他点，也分别有两条路径，因此一共有2×4=8种不同的走法。

故本题选A。
【2011-北京-080】

来源

合作链接 咨询电话：

合作链接
咨询电话：