[单选题]
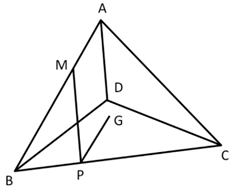
如图，A－BCD是棱长为3的正四面体，M是棱AB上的一点，且MB＝2MA，G是三角形BCD的重心，动点P在棱BC上，则PM+PG的最小值为：
A .
B .
C . 3
D .
参考答案： B
小麦参考解析：
第一步：判断题型------本题为几何问题
第二步：分析解题：
如下图所示，将面ABC和面BCD展开至一个平面。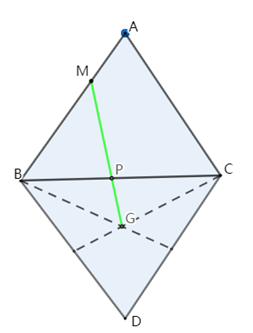
要想使MP+PG最小，应使MG为一条直线；
已知G是△BCD的重心，故BG平分∠CBD，所以∠GBC=30°，BG=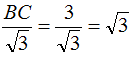
。
在△BMG中，已知∠MBG＝30°+60°=90°，MB=
AB=2。
所以
,即PM+PG的最小值为
。
故本题选B。
【2014-江苏A-040】
