[单选题]
【2019-上海A-061】
A . 8
B .
C .
D .
参考答案： D
小麦参考解析：
第一步：判断题型-------本题较长，所以优先考虑组合数列
第二步：题目详解
方法一：
将原数列奇偶项分组：
原数列奇数项组成的新数列：1、3、5、7，是公差为2的等差数列；
原数列偶数项组成的新数列：
，为分式数列；
分式数列分母依次为2、3、4，是公差为1的等差数列，下一项为4+1=5；
分子组成的新数列：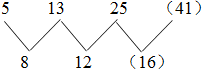
新数列相邻两项做差（后项-前项）为8、12、（），考虑公差为4的等差数列；
则下一项为12+4=16；
则原数列横线处数的分子为25+16=41，原数列横线处为
。
方法二：
将原数列每相邻两项两两分组为：（1，
）、（3，
）、（5，
）、（7，____）；
将每组的分母统一：（
，
）、（
，
）、（
，
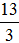）、（7，____）；
前三组分母依次为2、3、4，是公差为1的等差数列，则最后一组的分母为5；
最后一组分母统一为（
，
）；
每组的分子做差（后项分子-前项分子）得3、4、5，是公差为1的等差数列；
则最后一组两个数的分子的差则为6，最后一组后项的分子为35+6=41；
则原数列横线处为
。
故本题选D。
