[单选题]
某款游戏共有7名英雄供玩家选择，7名英雄的能力值恰好为1-7的不同整数。每局游戏开始前，玩家需要任选3名英雄进行组队。玩家阿坤在进行了无数次的组队尝试后发现，不能一味选择能力值高的英雄组队，只有当3名英雄的能力值平均数大于3且小于5时才能获胜。则阿坤在组队尝试过程中的胜率是（ ）。
A . 20%
B . 38%
C . 50%
D . 60%
参考答案： D
小麦参考解析：
第一步：判断题型------本题为概率问题
第二步：分析作答
三名英雄的能力值平均数在3到5之间才能获胜；
则三名英雄的能力总值在3×3=9到3×5=15之间，即10、11、12、13、14。
方法一：
情况较复杂，考虑枚举；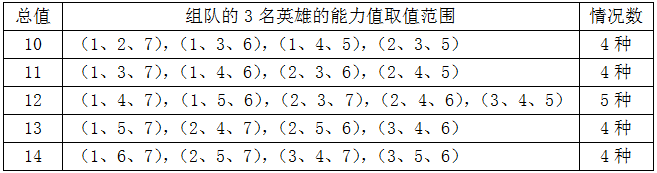
如上表所示，组队的三名英雄的总能力值在9到15之间的情况总数为4+4+5+4+4=21种；
组队的3名英雄的能力值取值情况总数为有
种；
则阿坤在组队尝试过程中的胜率是
。
方法二：
反向思考，不满足条件情况有两种：
（1）能力值之和小于等于9有（6、2、1）、（5、3、1）、（5、2、1）以及4及以下的4个数字（平均数必小于3）任意选择3个有
种，共3+4=7种；
（2）能力值之和大于等于15有（2、6、7）、（3、6、7）、（3、5、7）以及4及4以上的4个数字（平均数必大于5）任选3个有
种，共3+4=7种。
不满足的情况数一共有7+7=14种，总情况数有
种；
则满足三名英雄的能力值平均数在3到5之间概率为
，即阿坤在组队尝试过程中的胜率。
故本题选D。
【2020-深圳Ⅰ-055】
