[单选题]
12个人排成1列纵队,从前到后编为1~12号。现要将他们排成另一个与原来不同的纵队并从前到后重新编号,要求每个人的新号码与原始号码相差不超过1。那么有多少种重新编队的方法?
A . 155
B . 227
C . 232
D . 239
参考答案: C
小麦参考解析:
第一步:判断题型------本题为排列组合问题
第二步:分析解题
12个人重新排1列纵队,编为1~12号,要求每个人的新号码与原始号码相差不超过1,即≤1,那么每个人号码数不变,或者只与相邻的人交换号码。
除与原纵队号码一致的情况外,讨论不同人数交换情况,情况较复杂,枚举如下,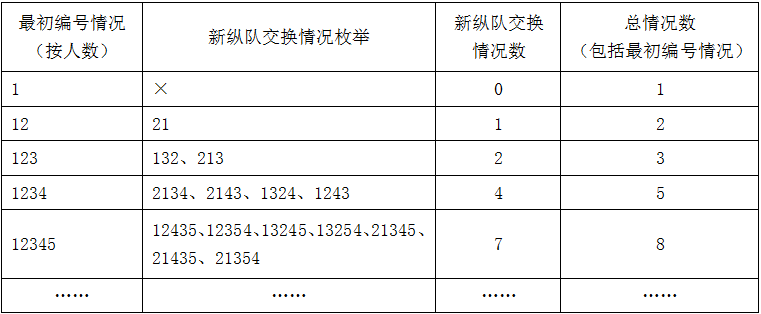
从表格得知,纵队每增加1人,总情况数为递推和数列,即1、2、3、5、8、13、21、34、55、89、144、233,因此12人的纵队加上初始编号总情况数为233种。
重新编队后不能与原纵队的顺序完全一致,则满足题意的情况数为233-1=232种。
故本题选C。
【2023-浙江A-070/浙江B-050/浙江C-050】



