某电商网站推出免息分期购物活动,购买某件商品的消费者第一个月只用支付总金额的一半加10元,第二个月支付剩余金额的一半加20元,第三个月支付剩余金额的一半加30元,第四个月付清剩余未支付的10元。问这件商品的价格为多少元?
400
410
420
460
民歌来源于民间主要以口头创作、口头流传、不断再创作的方式生存于民间,是一个国家、一个民族、一个地区人们思想感情的体验和表达手法的结晶。
下列关于民歌说法错误的是:
《诗经》是我国第一部诗歌总集
演唱藏族民歌常用乐器冬不拉伴奏
“信天游”是西北地区民歌形式
狩猎歌和牧歌是蒙古族民歌代表题材
马明、刘建、张义三个男同学各有一个妹妹,这天,六个人一起打羽毛球,举行的是男女混合双打,并且规定,兄妹俩人不搭伴。
第一盘对局的情况是:刘建和小萍对张义和小英。
第二盘对局的情况是:张义和小红对刘建和马明的妹妹。
根据题干的条件,以下哪项为真:
刘建和小红、马明和小英、张义和小萍各是兄妹
刘建和小英、马明和小萍、张义和小红各是兄妹
刘建和小萍、马明和小英、张义和小红各是兄妹
刘建和小红、马明和小萍、张义和小英各是兄妹
________指出:在一个家庭或在一个国家中,食物支出在收入中所占的比例随着收入的增加而减少。
恩格尔定律
科斯定理
凯恩斯主义
相对收入消费理论
某月中有三个星期一的日期都是偶数,则该月的18日一定是:
星期一
星期三
星期五
星期日
张先生在某个闰年中的生日是某个月的第四个也是最后一个星期五,他生日的前一个和后一个月正好也只有4个星期五。问当年的六一儿童节是星期几:
星期一
星期三
星期五
星期日
某校人数是一个三位数,平均每个班级36人,若将全校人数的百位数与十位数对调,则全校人数比实际少180人,那么全校人数最多可以达到多少人:
900
936
972
990
左图为给定的多面体,从任一角度观看,下面哪一项不可能是该多面体的视图:【2018国考地市077/国考副省081】
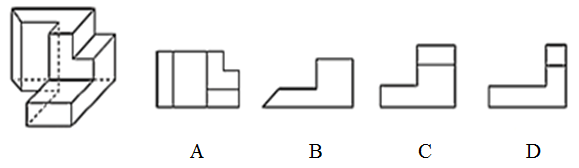
如图所示
如图所示
如图所示
如图所示
钱学森曾提出一个问题,后来被称为“钱学森之问”:为什么我们的学校总是培养不出杰出人才?虽然他当时只是针对科学研究而言,但这个问题可以推广到很多领域。比“钱学森之问”更为具体的问题是:相对于我们的人口规模,相对于我们的经济总量,相对于我们的教育投入,从我们的教育体制中走出来的具有创造力的人才,为什么这么少?
创造性思维首先来源于知识,这似乎没有争议。不过,对知识的界定需要更多思考。我们说的知识通常指学科和领域的专业知识。但是,知识也应该包括跨学科知识、跨领域知识、跨界知识。创造力多产生于学科交叉和融合。所以对“钱学森之问”的第一个回答是:学生的知识结构有问题,我们的学生过多局限于专业知识,而缺乏跨学科、跨领域、跨界知识,而这些往往是具有创造力的人才的特征。
创造性思维的第二个来源是好奇心和想象力。爱因斯坦说过,“________________”。他还说过,“________________”,在我们以知识为中心的教育中,这些知识以外的因素通常不受重视。知识与受教育年限的关系比较简单,通常随着受教育年限的增多而增多,但好奇心和想象力与受教育年限的关系则更取决于教育环境和教育方法。儿童时期的好奇心和想象力特别强,但是随着受教育的增多,好奇心和想象力很有可能会递减。这是因为,知识体系都是有框架、有假定的,难怪爱因斯坦感叹过,“________________”。如果这些分析是对的,那么对“钱学森之问”的第二个回答是:不是我们的学校培养不出杰出人才,而是我们的学校在增加学生知识的同时,有意无意地限制了创造性人才的必要因素——好奇心和想象力的发展。
创造性思维的第三个来源与价值取向有关,也就是与追求创新的动机和动力有关。创新的动机有三个层次,分别代表了三种价值取向:短期功利主义、长期功利主义和内在价值的非功利主义,每一个后者都比前者有更高的追求。对短期功利主义者而言,创新能够在短期带来奖励。对长期功利主义者而言,创新需要经过长期努力才能见到成效。而对内在价值的非功利主义者而言,创新源于一种内在动力,源自一种永不满足于现状的渴望,一种发自内心、不可抑制的激情,而不是为了个人的回报和社会的奖赏。现实情况是,具备第一类动机的人很多,具备第二类动机的人也有,但具备第三类动机的人就寥寥无几了。然而,科学和社会的殿堂中如果没有他们,就不成其为殿堂。所以,对“钱学森之问”的第三个回答是:我们之所以缺乏创造性人才,除了知识结构问题和缺乏好奇心和想象力之外,就是在价值取向上太“立竿见影”急于求成的心态,这样的价值观很难出现颠覆性创新、革命性创新。
将下列三个句子依次填入文中划横线处,正确的顺序是:
①我没有特殊的天赋,我只是极度地好奇
②好奇心能够在正规教育中幸存下来,简直就是一个奇迹
③想象力比知识更重要。因为知识只是局限于我们已知的一切,而想象力将包括整个世界中那些未知的一切
①②③
①③②
②③①
③②①
下列两组图形均由(1)(2)(3)三个图形组成,三个图形之间存在一定变化规律。按其规律右边这组图形中,图(3)应为:【2022上海B078】
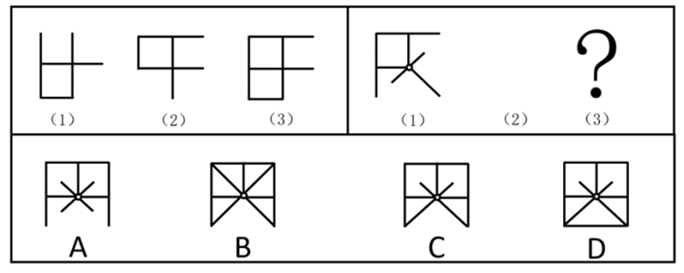
如图所示
如图所示
如图所示
如图所示

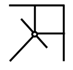 。图(1)与图(2)直接叠加得到?处图形,对应C选项。
。图(1)与图(2)直接叠加得到?处图形,对应C选项。 陕公网安备 61010302000399号
陕公网安备 61010302000399号