“我是歌手”某场比赛由六名首发歌手和一名踢馆歌手抽签决定出场顺序,且规定第一位出场和第七位出场歌手由踢馆歌手和上一场比赛第一名歌手抽取,剩余出场顺序由其他歌手抽取,则本场比赛出场顺序的排列共有多少种情况:
10080
120
240
6000
甲、乙两人从P,Q两地同时出发相向匀速而行,5小时后于M点相遇。若其他条件不变,甲每小时多行4千米,乙速度不变,则相遇地点距M点6千米;若甲速度不变,乙每小时多行4千米,则相遇地点距M点12千米。则甲、乙两人最初的速度之比为:
2:1
2:3
5:8
4:3
刚刚开学一个多星期,一名正在参加军训的大学生就将一大包衣服和七双袜子打包寄回家,让家人帮着洗,然后再寄回去。这则消息毫无悬念地引发了舆论的一阵喧哗,与以往类似的事情一样,痛心疾首者铺天盖地,上纲上线痛批中国教育的也不在少数。中国的校园总能不断地制造类似的奇闻轶事,高考和入学前后是集中爆发和展示期,年复一年,学校、孩子和家长似乎被符号化:学校一定是僵化冷漠且糟蹋人的,学生一定是娇生惯养未来要“垮掉”的,而家长多半是无原则的一味溺爱的。这样的符号化思维大大简化了中国社会以及中国教育的复杂性。
这段文字意在说明:
符号化的批评无助于教育和社会的进步
中国社会和学校的教育使学生缺乏独立性
社会舆论易对校园个别事例夸大宣传报道
大学生的独立性并不像媒体说的那么差
截止2022年底,中国位居全球风力发电装机总量第一位。下列与风力发电有关的说法错误的是:
目前新式风力发电机发出的电通常为交流电
风力发电的功率大小只取决于发电机的功率
风力发电机组主要由风轮、发电机和塔筒组成
全球风能总量远远超过可开发利用的水能总量
有一位数学家说:“很难想象一个文理不通、错字连篇的人,能把逻辑严谨的数学内涵表达出来。”著名数学家苏步青说:“我从小打好的语文基础,对我学习其他学科提供了很大的方便。我还觉得学好语文对训练一个人的思维很有帮助,可以使思想更有条理。这些,对我后来学好数学都有很大好处。”人们赞誉苏步青为“数学诗人”。
这段文字表达的是:
即使文理不通、错字连篇的人,也能把数学内涵表达出来
学好语文是学好数学的必备条件
数学家用亲身体会,明确地指出了学好语文的重要性
赞扬了“数学诗人”苏步青的惊人才华
有人说看电视会影响小学生的学习,可是对一所学校的调查发现,该校看电视时间较长的学生比看电视时间较短的学生的学习成绩好。由此看来,看电视不会影响小学生的学习。
以下哪项如果为真,最能削弱上面的推论:
该被调查学校的代表性不强
看电视可以开阔小学生的视野,增长他们的见识,有助于学习
该学校小学生的父母经常让孩子看一些具有教育意义的电视节目
该学校小学生的父母只在孩子取得了好成绩的时候才允许他们看电视
某旅游景点商场销售可乐,每买3瓶可凭空瓶获赠1瓶可口可乐,某旅游团购买19瓶,结果每人都喝到了一瓶可乐,该旅游团有多少人:
19
24
27
28
某中学计划抽调一批骨干教师前往西部地区支教,学校计划抽调2位高一老师、1位高二老师和1位高三老师,并且这4位老师所教科目应各不相同。已知各年级候选人如下:
①高一:历史老师甲、地理老师乙、政治老师丙。
②高二:地理老师丁、语文老师戊。
③高三:政治老师己、数学老师庚。则以下人选符合要求的是:( )。
甲、乙、丁、庚
甲、乙、戊、己
乙、丙、戊、己
乙、戊、己、庚
一家三口年龄各不相同,今年爸爸与妈妈年龄之和是孩子年龄的8倍,而10年后,爸爸与妈妈年龄之和为孩子年龄的5倍。今年爸爸、妈妈的年龄在各种可能组合中乘积最大,问今年妈妈的年龄可能是多少岁?
39
40
50
51
日常工作中,如果一件事发展得太过顺利,我们总会隐隐觉得有哪里不对,这样的直觉是有道理的。澳大利亚和法国的研究者们最近在某学术期刊上发表了一篇文章,说明了为什么当所有的证据都指向同一个结果时,它反而可能有问题。他们将此称之为“一致性悖论”。
研究者以证人指认犯人为例研究了一致性悖论,发现在辨认嫌疑人过程中,系统偏差可能来自多种心理偏差,如警方给证人展示照片的方式、证人自身的个人偏见等。而研究者发现,哪怕是细小的偏差都会对最终的整体结果产生极大影响。具体来讲,即使在1%的辨认过程中施加偏差,如暗示某人是犯人,最终当3个以上的证人意见一致时,他们的意见就不再可靠。有趣的是,如果_______,那么其他证人正确的概率反而会大大增加。
为什么会这样?可以用数学中的贝叶斯分析来说明。以扔硬币为例:如果我们有一枚硬币,扔到正面的概率为55%,而非普通硬币的50%,只要扔的次数足够多,就会发现正面向上多于反面向上的次数,进而发现这个硬币是有问题的。换句话说,当我们看到投掷结果中正面向上的次数显著多于反面向上时,就会意识到出问题的是硬币,而非概率定理。同样,根据概率定理,很多证人同时得到一致结论的可能性极低,所以更有可能的是系统出了差错。
在警方组织的嫌疑人指认中,指认同一个人有罪的证人数目越多,这个人真正有罪的概率就越大。然而,这只适用于没有任何系统偏差存在的理想情况。实际情况中,当指认同一个人为犯人的证人数目增加到一个值以后,该嫌疑人真正有罪的概率反而会下降,最终与随机指认毫无差别,且系统偏差越大,概率下降得越早。比方说,如果你让证人完成一项较为容易的任务,比如从一堆香蕉中找出一个苹果,所有人都几乎不会出错,多人结论一致的情况就可能出现,而指认犯人要比在一堆香蕉中找到苹果复杂得多。模拟显示,如果_______,他们认错人的概率会高达48%,在这种情况下,许多证人同时指认一个人为犯人的概率就相当低了;但如果_______,他们认错人的概率会大大降低,多个证人结论一致的情况出现的可能性也会提高。
在法律领域之外,一致性悖论还有很多用武之地,一个重要的应用就是加密技术。数据加密通常通过确认一个很大的数字是否为质数来进行,这个判断过程的错误率要达到非常低才行:低于2的负128次方才可以接受。在这一过程中,可能出现的系统差错就是计算机故障。大多数人都不会想到宇宙射线会导致电脑将一个合数误认为质数,毕竟这件事发生的概率只有10的负13次方——但要注意,这个概率要大于我们所要求的误差(2的负128次方),所以这类误差主导了整个过程的安全性。正因于此,加密协议所宣称的安全程度越高,实际的过程就越容易受计算机故障影响。
一致性悖论虽然听起来违背直觉,但研究者解释,一旦我们了解了足够的信息,就能理解它了。
第5段中“正因于此”的“此”,指的是:
加密技术判断过程的错误率并不可能达到2的负128次方
除宇宙射线外,还有其他因素会引起计算机的系统误差
上述加密技术的判断过程是在目前使用最为广泛的方法
出现计算机故障的概率高于加密技术判断过程的错误率
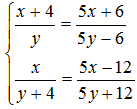 ,化简可得
,化简可得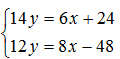 ,解得:x=2y;
,解得:x=2y;
 陕公网安备 61010302000399号
陕公网安备 61010302000399号