小李有一张银行卡，他忘记了密码的后3位，只记得这3个数全是奇数且有2个相同。问他尝试不超过两次就输入正确密码的概率为多少？
1/30
1/50
2/59
2/57
种情况；
种；
种。
；
，还剩59种情况，此时第二次输入正确得概率为
；
。
。
“80后”这个词，最早于2001年出现在网络论坛中，指的是一批活跃于网络论坛的出生于20世纪80年代的诗人。2003年开始，它更多指的是一批被商业运作出名的生于1980年以后的写手。2004年底，随着“80后作家”的批量涌现，这个词逐渐被用来指称整个20世纪80年代出生的年轻人群体。
最适合做这段文字标题的是：
“充满希望”的一代
“80后”的由来
用新视角理性看待“80后”
“80后”引起社会的广泛关注
数列：（3，5），（5，7），（11，13），（17，19），（29，31），（ ）
（41，43）
（57，59）
（61，65）
（71，73）
1/3，1/3，1/2，5/8，35/64，（ ）
75/128
85/256
175/576
315/1024
。
；
。2~3~13，3~8~25，5~14~41，8~22~（ ）
57
59
63
71
一个三位数的各位数字之和是16，其中十位数字比个位数字小3。如果把这个三位数的百位数字与个位数字对调，得到一个新的三位数，则新的三位数比原三位数大495，则原来的三位数是多少：
169
358
469
736
下列年份中，15~64岁人口占总人口比重最高的是（ ）年。
2013
2014
2015
2016
一个20人的班级举行百分制测验，平均分为79分，所有人得分都是整数且任意两人得分不同。班级前5名的平均分正好是16到20名平均分的2倍。则班级第6名和第15名之间的分差最大为多少分？
34
37
40
43
中世纪数学家比萨的莱奥纳多发现了斐波那契数列，它是这样一组数列：1、1、2、3、5······即后一数字为前面两个数字之和。那么，数列和树木的成长有什么关联呢？由于新生的枝条，往往需要一段“休息”时间，供自身生长，而后才能萌发新枝。所以，一株树苗在一段间隔，例如一年，以后长出一条新枝；第二年新枝“休息”，老枝依旧萌发；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则次年“休息”。这样，一株树木各个年份的枝桠数，便构成斐波那契数列。
这段文字意在说明：
斐波那契数列表现为树木的年轮增长
斐波那契数列在自然界中无处不在
斐波那契数列在自然中的应用
斐波那契数列表明植物在大自然中长期适应和进化
一个公比为2的等比数列，第n项与前n-1项和的差等于3，则此数列的前4项之和为：
54
45
42
36
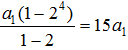，一定能被15整除；
陕公网安备 61010302000399号