(1)连降大雪
(2)形成雪灾
(3)家园被毁
(4)家园重建
(5)奋起自救
1-2-3-5-4
2-4-5-3-1
1-2-4-5-3
5-1-4-3-2
(1)夏朝灭亡
(2)商鞅变法
(3)统一六国
(4)周公吐哺
(5)卧薪尝胆
4-1-5-2-3
4-1-2-3-5
1-4-2-5-3
1-4-5-2-3
某学校组织一批学生乘坐汽车出去参观,要求每辆车上乘坐的学生人数相同,如果每辆车乘20人,结果多3人;如果少派一辆车,则所有学生正好能平均分乘到其他各车上,已知每辆汽车最多能乘坐25人,则该批学生人数是:
583
483
324
256
2019年3月,第四届联合国环境大会中国代表团和联合国环境规划署在肯尼亚首都内罗毕共同发布声明宣布,中国将主办2019年世界环境日活动,聚焦( )主题。
“可持续消费与生产”
“塑战塑决”
“空气污染”
“绿色经济”
(1)填写报名表
(2)考试
(3)查阅招考简章
(4)任职前公示
(5)体检
1—3—2—5—4
3—1—2—5—4
1—5—2—3—4
3—1—5—2—4
从3月下旬到10月上旬,太阳在地球上直射位置的移动规律是:
赤道→南回归线→赤道
赤道→北回归线→赤道
南回归线→赤道→北回归线
北回归线→赤道→南回归线
9,4,7,-4,5,4,3,-4,1,4,( ),( )
0,4
1,4
-1,-4
-1,4
2019年一季度,社会消费品零售总额97790亿元,同比名义增长8.3%(扣除价格因素实际增长6.9%,以下除特殊说明外均为名义增长)。其中,3月份社会消费品零售总额31726亿元,同比增长8.7%。
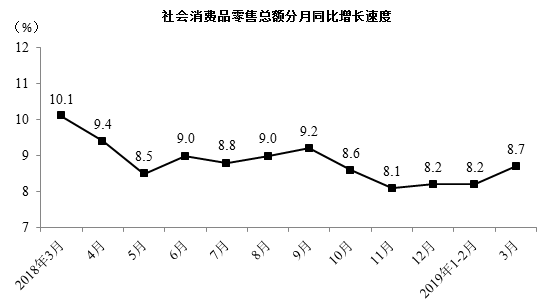
按经营单位所在地分,一季度城镇消费品零售额83402亿元,同比增长8.2%;乡村消费品零售额14388亿元,增长9.2%。其中,3月份城镇消费品零售额27192亿元,同比增长8.5%;乡村消费品零售额4534亿元,增长9.4%。
按消费类型分,一季度餐饮收入10644亿元,同比增长9.6%;商品零售87146亿元,增长8.2%。其中,3月份餐饮收入3393亿元,同比增长9.5%;商品零售28333亿元,增长8.6%。
按零售业态分,一季度限额以上零售业单位中的超市、百货店、专业店零售额同比分别增长7.5%、0.9%、3.9%,专卖店同比下降0.9%。
一季度,全国网上零售额22379亿元,同比增长15.3%。其中,实物商品网上零售额17772亿元,增长21.0%,占社会消费品零售总额的比重为18.2%;在实物商品网上零售总额中,吃、穿和用类商品分别增长24.6%、19.1%和21.3%。
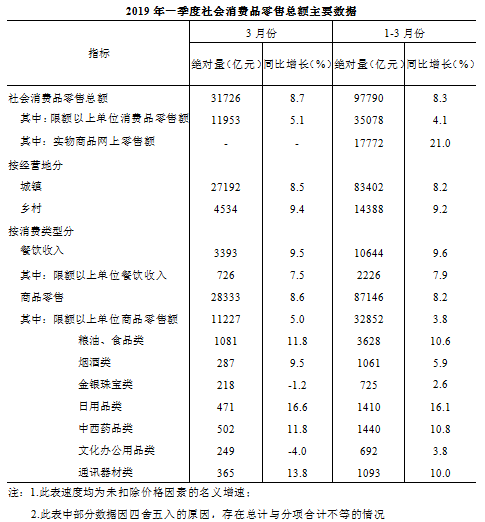
2018年1-3月,限额以上单位烟酒类、日用品类、中西药类及通讯器材类零售总额最高的是:
烟酒类
日用品类
中西药品类
通讯器材类
某汽车厂生产甲、乙、丙三种车型,其中乙型产量的3倍与丙型产量的6倍之和等于甲型产量的4倍,甲型产量与乙型产量的2倍之和等于丙型产量的7倍。则甲、乙、丙三型产量之比为:
5:4:3
4:3:2
4:2:1
3:2:1
日常工作中,如果一件事发展得太过顺利,我们总会隐隐觉得有哪里不对,这样的直觉是有道理的。澳大利亚和法国的研究者们最近在某学术期刊上发表了一篇文章,说明了为什么当所有的证据都指向同一个结果时,它反而可能有问题。他们将此称之为“一致性悖论”。
研究者以证人指认犯人为例研究了一致性悖论,发现在辨认嫌疑人过程中,系统偏差可能来自多种心理偏差,如警方给证人展示照片的方式、证人自身的个人偏见等。而研究者发现,哪怕是细小的偏差都会对最终的整体结果产生极大影响。具体来讲,即使在1%的辨认过程中施加偏差,如暗示某人是犯人,最终当3个以上的证人意见一致时,他们的意见就不再可靠。有趣的是,如果_______,那么其他证人正确的概率反而会大大增加。
为什么会这样?可以用数学中的贝叶斯分析来说明。以扔硬币为例:如果我们有一枚硬币,扔到正面的概率为55%,而非普通硬币的50%,只要扔的次数足够多,就会发现正面向上多于反面向上的次数,进而发现这个硬币是有问题的。换句话说,当我们看到投掷结果中正面向上的次数显著多于反面向上时,就会意识到出问题的是硬币,而非概率定理。同样,根据概率定理,很多证人同时得到一致结论的可能性极低,所以更有可能的是系统出了差错。
在警方组织的嫌疑人指认中,指认同一个人有罪的证人数目越多,这个人真正有罪的概率就越大。然而,这只适用于没有任何系统偏差存在的理想情况。实际情况中,当指认同一个人为犯人的证人数目增加到一个值以后,该嫌疑人真正有罪的概率反而会下降,最终与随机指认毫无差别,且系统偏差越大,概率下降得越早。比方说,如果你让证人完成一项较为容易的任务,比如从一堆香蕉中找出一个苹果,所有人都几乎不会出错,多人结论一致的情况就可能出现,而指认犯人要比在一堆香蕉中找到苹果复杂得多。模拟显示,如果_______,他们认错人的概率会高达48%,在这种情况下,许多证人同时指认一个人为犯人的概率就相当低了;但如果_______,他们认错人的概率会大大降低,多个证人结论一致的情况出现的可能性也会提高。
在法律领域之外,一致性悖论还有很多用武之地,一个重要的应用就是加密技术。数据加密通常通过确认一个很大的数字是否为质数来进行,这个判断过程的错误率要达到非常低才行:低于2的负128次方才可以接受。在这一过程中,可能出现的系统差错就是计算机故障。大多数人都不会想到宇宙射线会导致电脑将一个合数误认为质数,毕竟这件事发生的概率只有10的负13次方——但要注意,这个概率要大于我们所要求的误差(2的负128次方),所以这类误差主导了整个过程的安全性。正因于此,加密协议所宣称的安全程度越高,实际的过程就越容易受计算机故障影响。
一致性悖论虽然听起来违背直觉,但研究者解释,一旦我们了解了足够的信息,就能理解它了。
文中有3处画线部分,将以下3句依次填入,顺序正确的是:
①每个证人都曾经被犯人劫持为人质
②证人中有一个人与其他人的意见不合
③证人们都只在犯人逃走时匆匆瞥了一眼
①②③
②③①
③①②
②①③


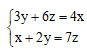 。
。 陕公网安备 61010302000399号
陕公网安备 61010302000399号