在一次职业技能竞赛中,六位决赛选手决出第一至第六的名次。一号选手比四号选手的名次低但比二号选手名次高;三号选手比二号选手名次低;五号选手的名次比三号选手的高但比四号选手的低。
根据下列哪项能够推出六号选手的名次比一号选手的名次低?
六号选手的名次比二号选手的名次低
六号选手的名次比三号选手的名次高
六号选手的名次比四号选手的名次低
六号选手的名次比五号选手的名次高
两个水桶一同被吊在井口上。其中一个对另一个说:“你看起来似乎闷闷不乐,有什么不愉快的事情吗?”另一个回答:“哎,我常在想,这真是一场徒劳,好没意思。常常是这样,才重新装满,随即又空着下来。”“啊,原来是这样。”第一个水桶说:“我倒不觉得如此。我一直是这样想:我们空空地来,装得满满地回去!”
这个故事告诉我们:
知足才能常乐
看问题的角度不同,看到的结果也不同
乐观的人生总能发现生活中的乐趣
换位思考,乐观待人
将以下图形序列中的哪两个调换位置之后,可以呈现出一定的规律性?【2013新疆079】

②和③
③和④
④和⑤
⑤和⑥
以下哪两个图形调换位置之后,使所有的图形能呈现出一定的规律性:【2019江西法检071】
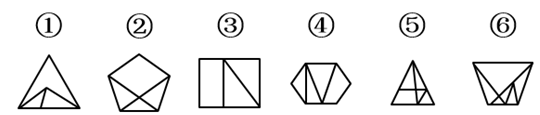
③和④
②和③
③和⑤
②和⑤
下面是某物体的两个侧面图,则该物体最可能是()。【2021广东思维能力064】
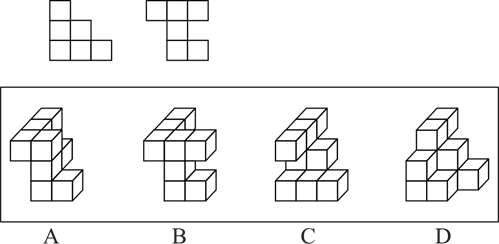
如图所示
如图所示
如图所示
如图所示
年终某单位评优,拟从所属甲、乙、丙、丁、戊、己、庚、辛8个部门中推选出12名候选人。要求:
(1)甲、乙、丁、辛4部门人数较少,4部门合计推选出2名候选人;
(2)没有合适人选的部门不必勉强推荐,有合适人选的部门至多可以推选出4名候选人;
(3)若甲、丙两部门至少有1个部门推选出候选人,则戊、己、庚3部门至多有1个部门可推选出候选人。
根据上述信息,可以得出下列______项中的两个部门均推选出了候选人。
戊和己
庚和辛
乙和丙
戊和丁
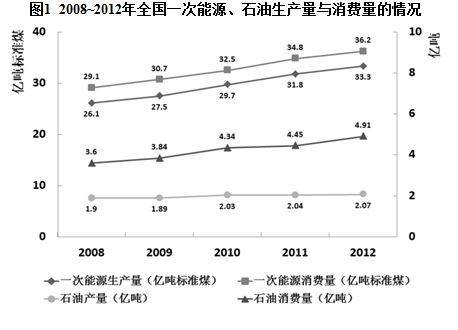
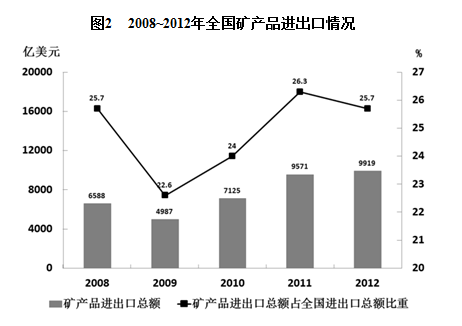
图中一次能源消费量与生产量差值最大的一年,该差值为多少亿吨标准煤:
2.9
3.0
3.1
3.2
有人认为,高考是很重要的考试,一年只有一次,应该让迟到考生进场考试。
如果以下各项为真,最能削弱上述观点的是:
不让迟到考生进场,有可能错失选拔优秀人才的机会
高考是很重要的考试,但并不一定会决定考生的命运
美国的高考—SAT考试,允许迟到的考生进场考试
遵守考场规则与考试的重要性、每年举行的次数无关
两个质量不同的小球被相同的力F同时从同一平台往水平方向扔出。假设忽略空气阻力,则以下说法正确的是:
两球在下落过程中离地面的高度始终一致
质量小的球扔出的距离会更短
两球在下落过程中的加速度不同
两球在下落过程中的速度相同
换个角度看问题,往往可以化难为易、化繁为简。一次,爱迪生让助手帮助自己测量一个梨形灯泡的容积,助手接过后,立即开始了工作,他一会儿拿游标卡尺测量,一会儿在稿纸上计算,后来甚至还动用了一些复杂的数学公式。可几个小时过去了,他忙得满头大汗,还是没有算出结果。就在助手搬出大学里学过的知识,准备再一次尝试计算灯泡的容积时,爱迪生进来了。爱迪生看到助手面前摆满的各种工具书和身旁的那一堆稿纸,立刻就明白了是怎么回事。于是,他拿起灯泡,朝里面倒满水,递给助手说:“你去把灯泡里的水倒进量杯里,就会得出我们所需要的答案。”这时,忙得满头大汗的助手才恍然大悟:自己想得太复杂了。看来,学会变通,善于让自己的思维转身是很重要的。
这段话主要支持了这样一种论点,即:
发明家区别于常人的重要品质是善于变通
学会变通,往往可以化难为易,化繁为简
做科研的方法过于单一,往往事倍功半
复杂的理论和公式的实用性比不上日常的生活经验

 陕公网安备 61010302000399号
陕公网安备 61010302000399号