某国的科研机构跟踪研究了出生于上世纪50至70年代的1万多人的精神健康状况,其间测试了他们在13岁至18岁时的语言能力、空间感知能力和归纳能力。结果发现,在此期间语言能力远低于同龄人水平的青少年,成年后患精神分裂症等精神疾病的风险较高。研究人员认为,青少年期语言能力的高低将是预测成年后精神疾病的重要指标。
以下哪项如果为真,能够质疑上述观点:
青少年期激素分泌水平异常,影响大脑发育,导致语言能力发展迟缓
患精神分裂症的青少年,其归纳能力相比语言能力的发展更加缓慢
许多精神健康的脑肿瘤患者在青少年时期也经常出现语言能力发展迟缓的问题
适当的教育可显著提高青少年的语言能力,但对中老年人影响不大
20世纪90年代以后,中国内地形成了一些跨省区市的经济区域:①长江三角洲和长江沿江地区经济带;②以广州、深圳为中心的珠江三角洲地区经济带;③包括北京、天津、河北、辽宁、山东、山西、内蒙古在内的环渤海地区经济区;④中部地区经济区,包括河南、湖北、湖南、安徽、江西。
上述经济区域形成的先后顺序是:
①②③④
②①④③
②④③①
④③①②
沙珠玉,曾是黄河上游风沙危害最严重的地区之一。20世纪50年代,沙珠玉九成草场已沙漠化。最严重的半年,沙丘向居民点推进了47米。_______,沙珠玉人开始_______。对他们来说,造林治沙,是一场用性命与风沙所做的生死搏斗。60多年来,沙珠玉人营造起18道防风林,层层叠叠的树木,硬生生将狂风顶住、逼沙丘后退。
依次填入划横线部分最恰当的一项是:
山穷水尽 孤注一掷
不进则退 迎难而上
退无可退 绝地反击
寸步难行 背水一战
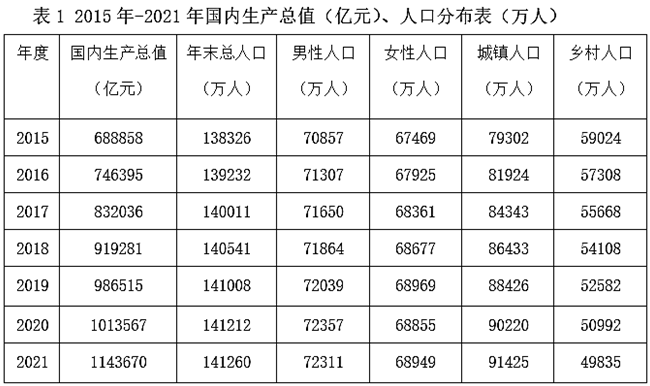
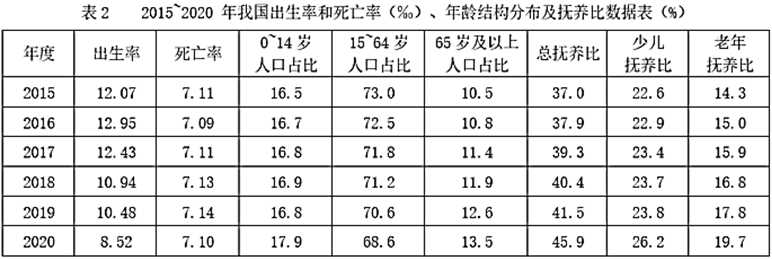
“十三五”期间(2016-2020年),人口自然增长率最高的年份是:
2016年
2017年
2018年
2019年
2017年末,全国医疗卫生机构床位794.0万张,其中:医院612.0万张(占77.1%),基层医疗卫生机构152.9万张(占19.3%)。医院中,公立医院床位占75.7%,民营医院床位占24.3%。与上年比较,床位增加53.0万张,其中:医院床位增加43.1万张,基层医疗卫生机构床位增加8.7万张。每千人口医疗卫生机构床位数由2016年5.37张增加到2017年5.72张。
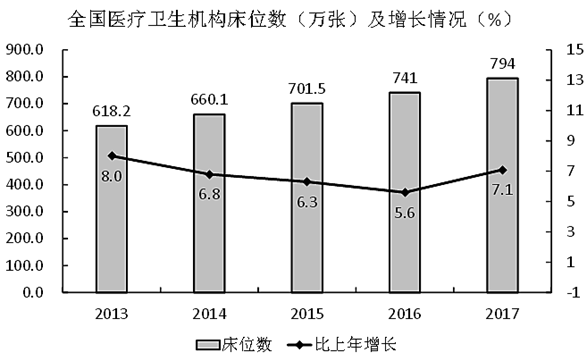
从所给数据资料中可以推算,2017年末全国人口总数比2016年末增加量最接近:
741万
822万
895万
938万
亚洲有中印两个人口大国,然而人口的庞大却与人才是否_______没有必然关系。人才供应缺口在一些国际化的行业中尤为_______,例如金融从业人员、工程研发人员等在全亚洲都供不应求。
填入划横线部分最恰当的一项是:
饱和 突出
充裕 明显
过剩 严峻
流失 巨大
一件可能使人感到吃惊的事实是,目前不但世界粮食产量的增长速度超过了人口的增长速度,而且同世界上人均收入的增长速度相比,粮食增长速度也是较快的,甚至其他商品价格的增长速度也比不上粮食的增长速度。尽管如此,今天在全世界仍有很多人口得不到充足的粮食。据估计,由于缺粮而面临饥饿的人口有3.4到7.3亿之多,他们尤其集中在南亚和非洲撒哈拉以南的地区。
这段文字想要说明的问题是:
世界粮食产量的增长速度超过了人口的增长速度
尽管世界粮食生产充足,但仍有很多人口得不到充足的粮食
其他产品价格的增长速度比不上粮食的增长速度
因缺粮而面临饥饿的人口有3.4到7.3亿之多
大约公元前450年,古希腊哲学家阿那克萨哥拉提出一个有趣的问题:只用直尺和圆规,能否作出一个与给定圆面积相等的正方形?这个看似简单的“化圆为方”问题成为尺规作图领域的经典题目,在此后的两千多年中,许多数学家尝试解答却都未能成功。这个问题之所以难以解答,在于它不仅是一个几何学问题,还是一个代数学问题。在尺规作图问题中,给定若干角度或线段长度,实质是给出了若干实数;只用直尺和圆规作图这条规则,保证了作出的角度或线段的长度,是给定实数的和、差、积、商、平方根的组合。因此每个尺规作图问题,其实都对应着一个代数问题。
关于“化圆为方”问题,文中没有谈到:
提出问题的具体背景
关于问题实质的分析
问题难以解答的原因
对该问题的大体描述
上世纪70年代,湖南长沙马王堆汉墓出土了12万字以上的帛书,其中有一部失传已久的《相马经》,是我国动物学、畜牧学的重要文献。春秋战国时期,由于已从车战演变到骑兵作战,马的身价愈来愈高。传说中的相马专家是伯乐,事实上,这类专家数量众多,《吕氏春秋》就提到十个相马家,《史记》也提到“以相马立名天下”的人士,这些都可以证明古人对相马的重视。
下列说法与原文相符的是:
相马技术的发展使得车战逐渐被淘汰
《相马经》是伯乐所撰写的相马学专著
相马术的出现推动了古代动物学的发展
相马师这一职业早在汉代以前就已经出现
有三个孩子分别叫婷婷(女)、笑笑(女)和强强。孩子的妈妈分别是孙梦甜、蒋英英和齐怀瑾。邻居张奶奶说:“冯一坤和蒋英英的孩子都参加了小学女子合唱团,周丹心的女儿不是笑笑,楚中天和齐怀瑾不是一家人。”
由此可以推断出下列是一家人的是:
周丹心、蒋英英和笑笑,楚中天、孙梦甜和婷婷
楚中天、孙梦甜和强强,冯一坤、齐怀瑾和笑笑
周丹心、齐怀瑾和笑笑,楚中天、蒋英英和强强
楚中天、齐怀瑾和笑笑,冯一坤、孙梦甜和强强

 陕公网安备 61010302000399号
陕公网安备 61010302000399号