某学院在开学之初,利用4天时间开设了哲学、逻辑、数学、统计、宗教、历史和艺术7门课程让学生试听。每天上午、下午各一门。除一门课程可以开设两次之外,其他课程均不重复。这4天的课程设置还须满足以下条件:
(1)艺术课程至少有一次安排在第3天;
(2)数学课程只能安排在逻辑课程的次日;
(3)第1天或第2天中至少有一天安排统计课程;
(4)哲学课程与数学课程或艺术课程安排在同一天;
(5)开设两次的课程不能安排在同一天,也不能安排在第3天,其中一次要安排在第4天。
以下哪门课程不能开设两次:
哲学
逻辑
统计
历史
某地举办铁人三项比赛,全程为51.5千米,游泳、自行车、长跑的路程之比为3:80:20。小陈在这三个项目花费的时间之比为3:8:4,比赛中他长跑的平均速度是15千米/小时,且两次换项共耗时4分钟,那么他完成比赛共耗时多少:
2小时14分
2小时24分
2小时34分
2小时44分
某商场出售甲、乙两种不同价格的笔记本电脑,其中甲电脑连续两次提价10%,乙电脑连续两次降价10%,最后两种电脑均以9801元售出各一台,与价格不升不降比较,则商场盈亏情况是( )。
不赚不亏
少赚598元
多赚980.1元
多赚490.05元
甲、乙、丙、丁4位同学参加学校运动会。已知,他们4人每人都至少获得1个奖项,4人获奖总数为10。关于具体获奖情况,4人还有如下说法:
甲:乙和丙的获奖总数为5;
乙:丙和丁的获奖总数为5;
丙:丁和甲的获奖总数为5:
丁:甲和乙的获奖总数为4。
后来得知,获得2个奖项的人说了假话,而其他人均说了真话。
根据以上信息,甲、乙、丙、丁4人具体的获奖数分别应是:
2、3、2、3
2、4、1、3
2、2、2、4
2、2、3、3
2021年3—5月某市共享单车使用情况如下:
2021年3—5月全市共投入120万辆共享单车,其维修率约为10%。维修量同比减少5%,其平均使用率为92%,同比增长2个百分点。
2021年3月,甲公司共投入12万辆共享单车,其占全市当月投入共享单车总量的比率比乙公司的高3个百分点;甲公司当月投入共享单车的使用率为90%,比乙公司的低2个百分点。
2021年4月,乙公司当月投入的共享单车维修了0.9万辆,其维修率为9%,环比减少了2个百分点。甲公司当月投入的共享单车维修了1.1万辆,其维修率为12%,环比增长了4个百分点。
2021年5月,乙公司当月投入共享单车13.5万辆,占全市当月投入共享单车总量的30%,环比增长1个百分点,乙公司当月投入共享单车的使用率为95%,环比增长3个百分点。
2021年4—5月,乙公司在该市共投入共享单车多少万辆?
10
13.5
21.6
23.5
一个公比为2的等比数列,第n项与前n-1项和的差等于5,则此数列前4项之和为:
70
85
80
75
某新建农庄有一项绿化工程,交给甲、乙、丙、丁4人合作完成。已知4人的工作效率之比为3∶5∶4∶6,甲乙合作完成所需时间比丙丁合作多9天,则4人合作完成工程所需时间是:
17天
18天
19天
20天
某超市下午3点开始对其新上架的洗发液进行半价促销,并规定之后每次整点时,洗发液的价格都会上调其原价的5%,直至恢复原价。张大妈4点15分在超市抢购了2瓶,6点半又去超市买了2瓶。张大妈两次购买洗发液共花费48元,问与原价相比共节省了多少元?
12
24
32
48
谷子大约在5000万年前开始从水稻中分化出来,分化之后的基因组结构仍存在明显的共线性。研究人员发现谷子的2号和9号染色体分别由水稻的7号和9号,3号和10号染色体融合而成。同时,他们发现这两次融合事件也发生在高粱的染色体中,由此,研究人员推测这两次染色体融合事件应该发生在高粱从谷子中分化出来之前。
上述推理需要以下哪项作为前提:
高粱从谷子中分化出来发生在谷子从水稻中分化出来之后
高粱与谷子之间的共线性小于高粱和水稻之间的共线性
3号和10号染色体融合之后不大可能再分离开来
谷子由水稻分化出来之后又发生一次染色体融合事件
某研究将行走模式分为两类:一类是零星地短时间行走,另一类是不间断地行走10分钟以上。该研究追踪了某国16732名66岁至78岁女性,4年随访期间有804名女性去世。结果发现,不管是零星散步还是较长时间的不间断行走,步数更多的人寿命更长;在约4500步之后,这种效应趋于稳定。研究者提出,只要开始走路,就能降低老年女性死亡风险。
以下各项如果为真,哪项不能质疑研究者的结论?
中青年女性的生活方式和老年女性有很大不同,每天行走步数与死亡率没有显著关联
正确的走路方式,才能使身体变得健壮,不当的走路方式和姿势,会危害身体健康
在这个年龄段,每天能够自主行走达到一定步数,通常意味着有更好的整体健康状况
能够坚持走路的人,或者有更多的生活内容,或者有更好的健康意识,这两者均有益健康





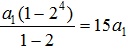 ,一定能被15整除;
,一定能被15整除; 陕公网安备 61010302000399号
陕公网安备 61010302000399号