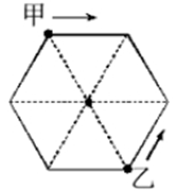
一个正六边形跑道,每边长为100米,甲、乙两人分别从两个相对的顶点同时出发,沿跑道相向匀速前进。第一次相遇时甲比乙多跑了60米,问甲跑完三圈时,两人之间的直线距离是多少:
100米
150米
200米
300米
A、B两桶中共装有108公斤水。从A中取出![]() 的水倒入B,再从B中取出
的水倒入B,再从B中取出![]() 的水倒入A,此时A、B两桶水重量刚好相等,那么B中原来有多少公斤水?
的水倒入A,此时A、B两桶水重量刚好相等,那么B中原来有多少公斤水?
42
48
50
60
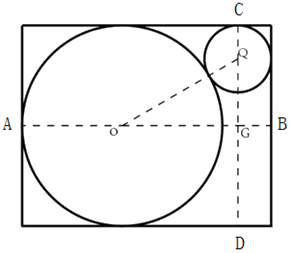
某地打算在绿地上建两个圆形花坛,如下图所示,大圆的直径为6米,小圆的直径为2米,修建期间暂时在外围设置围栏。已知围栏呈矩形,大圆与围栏的三条边相切,小圆与围栏的两条边相切,且两圆相切,那么矩形围栏的面积是多少平方米?

![]()
![]()
![]()
![]()
甲乙两辆车从A地驶往90公里外的B地,两车的速度比为5:6,甲车于上午10点半出发,乙车于10点40分出发,最终乙车比甲车早2分钟到达B地。问两车的时速相差多少千米/小时:
10
12
12.5
15
5名职工在办公室里的分机号码都是2位数字,且他们分机号码最后一位的5个数字相加为32,最大的数比最小的大7且各不相同。如将每个人的分机号码个位和十位颠倒形成新的分机号,则5个人新分机号码的5个2位数字之和最大为:
365
395
482
495
某省游泳队进行了为期一个月的高原集训,集训最后一日所有队员进行了一次队内测试,几位教练预测了一下队员的成绩:
张教练说:这次集训时间短,没人会达标。
孙教练说:有队员会达标。
王教练说:省运会冠军或国家队队员可达标。
测试结束后,只有一位教练的预测是正确的。
由此可以推出:
没有人达标
全队都达标了
省运会冠军达标
国家队队员未达标
小明和小华计算甲、乙两个不同自然数的积(这两个自然数都比1大)。小明把较大的数字的个位数错看成了一个更大的数字,其计算结果为144,小华却把乘号看成了加号,其计算结果为28。问两个数的差为:
16
12
8
4
甲、乙两人卖数量相同的萝卜,甲打算卖1元2个,乙打算卖1元3个。如果甲、乙两人一起按2元5个的价格卖掉全部的萝卜,总收入会比预想的少4元钱。问两人共有多少个萝卜:
420
120
360
240
凡是有利于两岸关系和平发展的事都应该大力推动,凡是破坏两岸关系和平发展的事都必须坚决反对。
据此,可以推出:
凡应该大力推动的事都是有利于两岸关系和平发展的事
凡必须坚决反对的事都是破坏两岸关系和平发展的事
有些不利于两岸关系和平发展的事不应该大力推动
有些不破坏两岸关系和平发展的事必须坚决反对
19世纪,爱默生和其他一些作家向读者传授一种称为“自助论”的理论。在这些人看来,一个有个性的人必须要有一颗充实的大脑。在这种思想的指导下,为了得到他人的尊重,有必要在闲暇时广泛涉猎文化史上的杰出著作。同时,也有必要熟悉哲学、神学和世界范围内的重大政治事件。这种风气在一个多世纪的时间里塑造了美国新闻业。在那几十年里,杂志致力于推广古典歌剧、高雅艺术和宗教神学,而不是电影或大众健康常识。
这段文字意在说明:
新闻媒体是主流文化观的集中体现
广泛阅读可以充实我们的大脑
主流媒体有引导大众品味的责任
自助论为美国新闻业的发展提供了方向
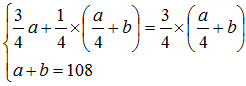 ,解得
,解得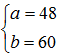 。
。

 陕公网安备 61010302000399号
陕公网安备 61010302000399号