某街道常住人口与外来人口之比为1:2,已知该街道下辖的甲、乙、丙三个社区人口比为12:8:7。其中,甲社区常住人口与外来人口比为1:3,乙社区为3:5,则丙社区常住人口与外来人口比为:
2:3
1:2
1:3
3:4
甲、乙、丙、丁四位同学正在商量小组作业的分工,他们当中一个人负责宣传资料,一个人负责收集素材,一个人负责写发言稿,一个人负责录制短视频。已知:
①乙不负责宣传资料,也不负责写发言稿
②甲不负责宣传资料,也不负责录制短视频
③丁不负责写发言稿,也不负责录制短视频
④丙不负责录制短视频,也不负责宣传资料
⑤如果甲不负责写发言稿,那么丁不负责宣传资料
那么负责收集素材的是:
甲
乙
丙
丁
航天局认为优秀宇航员应具备三个条件:第一,丰富的知识;第二,熟练的技术;第三,坚强的意志。现在至少符合条件之一的甲、乙、丙、丁四位优秀飞行员报名参选,已知:
①甲、乙意志坚强程度相同;
②乙、丙知识水平相当;
③丙、丁并非都是知识丰富;
④四人中三人知识丰富,两人意志坚强,一人技术熟练。
航天局经过考察,发现其中只有一人完全符合优秀宇航员的全部条件。他是:
甲
乙
丙
丁
2005年全国1%人口抽样调查数据显示,至2005年11月1日零时全国31个省、自治区、直辖市和现役军人的总人口为130628万人,比2000年11月1日零时第五次全国人口普查的总人增加了4045万人,增长3.2%;年平均增加809万人,年平均增长0.63%。
其中,居住在城镇的人口56457万人,居住在乡村的人口74471万人:男性67309万人,女性63319万人;具有大学程度(指大专及以上)的人口为6764万人,高中程度(含中专)的人口为15083万人,初中程度的人口为46735万人,小学程度的人口为40706万人。另外,0–14岁的人口为26478万人,占总人口的20.27%;15–59岁的人口为89742万人,占总人口的68.70%;60岁及以上的人口为14408万人,占总人口的11.03%(其中:65岁及以上的人口为10045万人,占总人口的7.69%)。
至2005年11月1日零时,我国完成九年义务教育的人口占总人口数的:
52.5%
66.9%
16.7%
31.1%
有一堆棋子(棋子数大于1),把它们四等分后剩一枚,拿去三份零一枚,将剩下的棋子再四等分后还是剩一枚,再拿去三份零一枚,将剩下的棋子四等分还是剩一枚。问原来至少有多少枚棋子:
23
37
65
85
某项射击资格赛后的统计表明,某国四名运动员中,三名运动员的平均环数加上另一运动员的环数,计算后得到的环数分别为92、114、138、160,则此国四名运动员资格赛的平均环数是:
63
126
168
252
众数是一组数据中出现次数最多的一个数据。平均数是一组数据中表示平均每份的数量。中位数是一组数据按大小顺序排列,位于最中间的一个数据。
根据上述定义,下列说法错误的是:
平均数说明的是整体的平均水平,中位数说明的是生活中的中等水平
日常生活中诸如“最佳”“最受欢迎”的评选,一般都与众数有关系
平均数通过计算得出,中位数通过排序得出,众数是通过计数得出的
个别极端数据对平均数的影响不明显,对众数和中位数的影响则较大
某超市出售1.5升装和4升装两种规格的矿泉水,1.5升装的每瓶进价3元,售价4.5元;4升装的每瓶进价7元,售价9元,三月份该超市共出售1000升矿泉水,利润(总售价-总进价)为800元。问售出1.5升装矿泉水的瓶数是4升装的几倍?
4
3
2
1.5
某公司举办年终晚宴,每桌安排7名普通员工与3名管理人员,到最后2桌时,由于管理人员已经安排完毕,便全部安排了普通员工,结果还是差2人才刚坐满,已知该公司普通员工数是管理人员的3倍,则该公司有管理人员多少名:
24
27
33
36
中世纪数学家比萨的莱奥纳多发现了斐波那契数列,它是这样一组数列:1、1、2、3、5······即后一数字为前面两个数字之和。那么,数列和树木的成长有什么关联呢?由于新生的枝条,往往需要一段“休息”时间,供自身生长,而后才能萌发新枝。所以,一株树苗在一段间隔,例如一年,以后长出一条新枝;第二年新枝“休息”,老枝依旧萌发;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则次年“休息”。这样,一株树木各个年份的枝桠数,便构成斐波那契数列。
这段文字意在说明:
斐波那契数列表现为树木的年轮增长
斐波那契数列在自然界中无处不在
斐波那契数列在自然中的应用
斐波那契数列表明植物在大自然中长期适应和进化
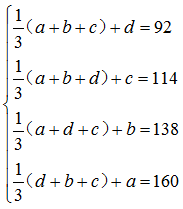 ,解得a+b+c+d=252;
,解得a+b+c+d=252;
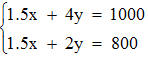
 陕公网安备 61010302000399号
陕公网安备 61010302000399号