2,3,10,15,26,( )
30
35
38
57
-26,-6,2,4,6,( )
16
12
14
6
大约公元前450年,古希腊哲学家阿那克萨哥拉提出一个有趣的问题:只用直尺和圆规,能否作出一个与给定圆面积相等的正方形?这个看似简单的“化圆为方”问题成为尺规作图领域的经典题目,在此后的两千多年中,许多数学家尝试解答却都未能成功。这个问题之所以难以解答,在于它不仅是一个几何学问题,还是一个代数学问题。在尺规作图问题中,给定若干角度或线段长度,实质是给出了若干实数;只用直尺和圆规作图这条规则,保证了作出的角度或线段的长度,是给定实数的和、差、积、商、平方根的组合。因此每个尺规作图问题,其实都对应着一个代数问题。
关于“化圆为方”问题,文中没有谈到:
提出问题的具体背景
关于问题实质的分析
问题难以解答的原因
对该问题的大体描述
南北向的铁路旁有一条平行的公路,公路经过A镇,有一行人与一骑车人早上同时从A镇沿公路向南出发。行人的速度为7.2千米/小时,骑车人的速度为18千米/小时。同时,有一列火车从他们背后驶来,9点10分恰好追上行人,而且从行人身边通过用了20秒;9点18分恰好追上骑车人,从骑车人身边通过用了26秒。则二人从A镇出发时,火车离A镇还有()千米。
15.8
18.6
20.8
24.0
13,33,26,28,( ),86
47
57
68
76
过去100多年来,围绕达尔文进化论是否正确的争论从未停歇。不断涌现的科学事实在弥补达尔文当年未曾发现的“缺失环节”的同时,也在检验着达尔文进化论的预测能力。例如,2004年在加拿大发现的“提克塔利克鱼”化石揭示了从鱼类(鳍)到陆生动物(腿)之间的过渡状态,被公认是“种系渐变论”的一个极好例证。当然,达尔文进化论并非完美无缺,它确实存在“可证伪”之处。以自然选择理论为例,它在孟德尔遗传学建立之初就受到了强烈挑战,但各种不能用自然选择理论简单解释的新证据最终还是拓展了人们对进化动力和机制的认识,而不是摒弃该理论。
这段文字以自然选择理论受到孟德尔遗传学挑战为例,目的是:
说明达尔文进化论具有可证伪性
证明达尔文进化论具有预测能力
提出“种系渐变论”的事实例证
加深人们对生物进化机制的认识
13,17,26,( ),67,103
28
36
42
45
根据伯努利效应,当流体经过物体表面时,流速较快的一面压力越小,流速越慢的一面压力越大,当物体两面的压力差达到一定程度时,便会发生位移。以下物体没有利用伯努利效应的是:
赛车尾翼
飞机机翼
潜艇外壳
帆船船帆
马克思说:“蒸汽、电力和自动纺织机甚至是比巴尔贝斯、拉斯拜尔和布朗基诸位公民更危险万分的革命家。”这一论断的含义是:
科技革命对统治者的地位有威胁
科技革命会导致政治变革
科技革命对社会变革有直接决定作用
滥用科技革命的成果会给人类带来危险
0,2,7,4,26,6,63,8,( )
124
9
71
99
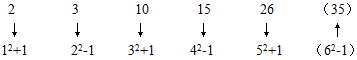


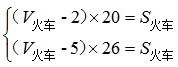 ,解得
,解得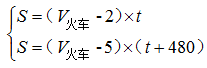 ,解得S=20800米=20.8千米。
,解得S=20800米=20.8千米。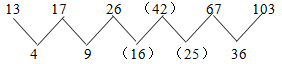
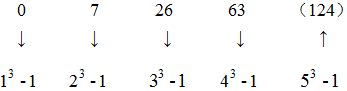
 陕公网安备 61010302000399号
陕公网安备 61010302000399号