2020年1月李某因意外事件下落不明,2022年3月李某的丈夫盛某向法院申请宣告李某死亡,法院于2022年4月10日作出判决。2022年8月,李某返回家中,发现盛某已与另一名女子杜某结婚,自己的女儿已被朋友艾某收养。下列与之相关的说法错误的是:
艾某收养李某女儿的行为继续有效
李某可以向法院申请撤销死亡宣告
李某与盛某的婚姻关系不能自行恢复
李某在2020年1月至2022年8月期间实施的民事法律行为无效
在下列4×4的正方形矩阵中,每个小方格可填入一个汉字,要求每行每列以及粗线框成的4个小正方形中均含有天、地、日、月4个汉字。
根据上述条件,方格①中应填入的汉字是:
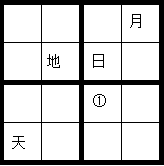
地
天
月
日
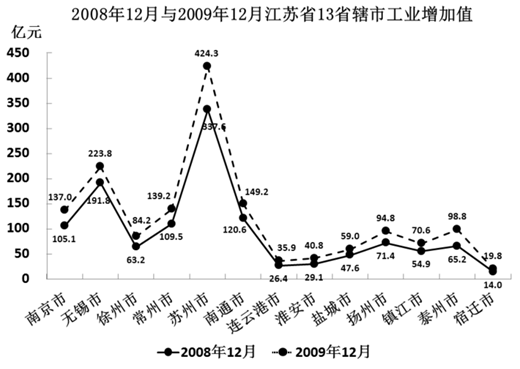
下列分析不正确的有:
(1)2009年12月扬州市工业增加值同比增长了32.77个百分点。
(2)按2009年的月平均增量估算,2010年4月南通市工业增加值可望达到158.7亿元。
(3)2009年12月江苏省各省辖市工业增加值均比2008年12月至少增加8亿元。
0个
3个
2个
1个
2016年,我国全年完成邮电业务收入总量43344亿元,比上年增长52.7%。其中,邮政业务收入7397亿元,增长45.7%;电信业务收入35947亿元,增长54.2%。邮政业全年完成邮政函件业务36.2亿件,包裹业务0.3亿件,快递业务量312.8亿件;快递业务收入3974亿元。电信业全年新增移动电话交换机容量7318万户,达到218384万户。2016年末全国电话用户总数152856万户(电话包括固定电话和移动电话两种),其中移动电话用户132193万户。移动电话普及率上升至96.2部/百人。固定互联网宽带接入用户29721万户,比上年增加3774万户,其中固定互联网光纤宽带接入用户22766万户,比上年增加7941万户;移动宽带用户94075万户,增加23464万户。移动互联网接入流量93.6亿G,比上年增长123.7%。互联网上网人数7.31亿人,增加4299万人,其中手机上网人数6.95亿人,增加7550万人。互联网普及率达到53.2%,其中农村地区互联网普及率达到33.1%。软件和信息技术服务业完成软件业务收入48511亿元,比上年增长14.9%。
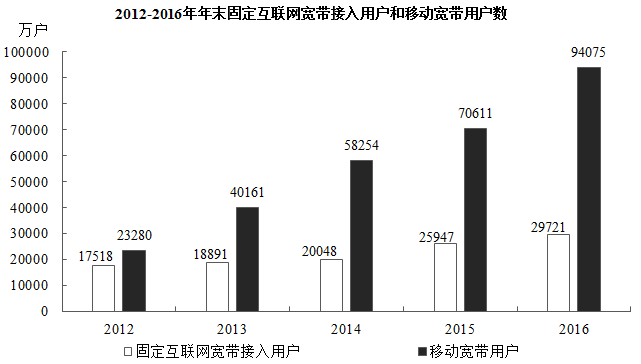
关于我国邮电业务情况的说明,下列说法正确的是:
2015年末,我国固定互联网光纤宽带接入用户与移动宽带用户的差额低于50000户
2016年固定互联网宽带接入用户同比增长率高于移动宽带用户增长率
2016年末,我国使用固定电话的总人数比移动电话的多
2016年我国城市地区互联网普及率已超过一半
某校辩论队的小赵、小钱、小孙和小李分别是哲学、中文、历史和英语专业的,他们也都爱好下围棋。还知道如下情况:
(1)小孙和历史专业的下过围棋,并且各有输赢;
(2)哲学专业的只和中文专业的下过围棋,而且从没赢过;
(3)小钱和小孙二人曾和哲学专业的同学一起爬过山;
(4)某日小李、小赵下围棋,且小赵取胜。
据此,可以推出:( )。
小赵是学英语的,小钱是学历史的
小钱是学历史的,小孙是学中文的
小赵是学历史的,小孙是学英语的
小李是学哲学的,小钱是学历史的
考入蓝天外国语学校的学生,一般都被认为是学霸级人物。虽然聪明、勤奋的同学未必都能成为蓝天外国语学校的学生,但是蓝天外国语学校的学生多半聪明或勤奋。
根据以上陈述,可以得出以下哪项:
有的聪明、勤奋的同学必然不会成为蓝天外国语学校的学生
有的聪明、勤奋的同学可能不会成为蓝天外国语学校的学生
大多数蓝天外国语学校的学生既聪明又勤奋
有少数蓝天外国语学校的学生既聪明又勤奋
日常工作中,如果一件事发展得太过顺利,我们总会隐隐觉得有哪里不对,这样的直觉是有道理的。澳大利亚和法国的研究者们最近在某学术期刊上发表了一篇文章,说明了为什么当所有的证据都指向同一个结果时,它反而可能有问题。他们将此称之为“一致性悖论”。
研究者以证人指认犯人为例研究了一致性悖论,发现在辨认嫌疑人过程中,系统偏差可能来自多种心理偏差,如警方给证人展示照片的方式、证人自身的个人偏见等。而研究者发现,哪怕是细小的偏差都会对最终的整体结果产生极大影响。具体来讲,即使在1%的辨认过程中施加偏差,如暗示某人是犯人,最终当3个以上的证人意见一致时,他们的意见就不再可靠。有趣的是,如果_______,那么其他证人正确的概率反而会大大增加。
为什么会这样?可以用数学中的贝叶斯分析来说明。以扔硬币为例:如果我们有一枚硬币,扔到正面的概率为55%,而非普通硬币的50%,只要扔的次数足够多,就会发现正面向上多于反面向上的次数,进而发现这个硬币是有问题的。换句话说,当我们看到投掷结果中正面向上的次数显著多于反面向上时,就会意识到出问题的是硬币,而非概率定理。同样,根据概率定理,很多证人同时得到一致结论的可能性极低,所以更有可能的是系统出了差错。
在警方组织的嫌疑人指认中,指认同一个人有罪的证人数目越多,这个人真正有罪的概率就越大。然而,这只适用于没有任何系统偏差存在的理想情况。实际情况中,当指认同一个人为犯人的证人数目增加到一个值以后,该嫌疑人真正有罪的概率反而会下降,最终与随机指认毫无差别,且系统偏差越大,概率下降得越早。比方说,如果你让证人完成一项较为容易的任务,比如从一堆香蕉中找出一个苹果,所有人都几乎不会出错,多人结论一致的情况就可能出现,而指认犯人要比在一堆香蕉中找到苹果复杂得多。模拟显示,如果_______,他们认错人的概率会高达48%,在这种情况下,许多证人同时指认一个人为犯人的概率就相当低了;但如果_______,他们认错人的概率会大大降低,多个证人结论一致的情况出现的可能性也会提高。
在法律领域之外,一致性悖论还有很多用武之地,一个重要的应用就是加密技术。数据加密通常通过确认一个很大的数字是否为质数来进行,这个判断过程的错误率要达到非常低才行:低于2的负128次方才可以接受。在这一过程中,可能出现的系统差错就是计算机故障。大多数人都不会想到宇宙射线会导致电脑将一个合数误认为质数,毕竟这件事发生的概率只有10的负13次方——但要注意,这个概率要大于我们所要求的误差(2的负128次方),所以这类误差主导了整个过程的安全性。正因于此,加密协议所宣称的安全程度越高,实际的过程就越容易受计算机故障影响。
一致性悖论虽然听起来违背直觉,但研究者解释,一旦我们了解了足够的信息,就能理解它了。
根据本文,下列哪种情况中可能存在一致性悖论:
检测站对某公司生产的所有新车及使用5年以上的旧车分别进行了尾气检测,检测结果为该公司生产的新车均达到尾气排放标准
低空跳伞世界级选手辛普森有2000次高空跳伞和1400次低空跳伞的经历,但是,他的第1401次低空跳伞,因降落伞未打开而以失败告终
两个城市的两位彩民凭借机选票分享一等奖两注,这两张在同一分钟购买的彩票,不仅中大奖那注号码一致,没中奖的两注机选号码也完全一致
在欧洲殖民者发现澳大利亚的黑天鹅之前,欧洲人曾经认为天鹅都是白色的,后来欧洲人登陆澳大利亚后,一上岸竟发现有黑色的天鹅
数列:(1,1,1),(2,2,4),(3,4,12),(4,8,32),……,第8个括号内最后一个数是( )。
256
512
1024
2048
2016年3月,阿尔法围棋程序(AlphAGo)对战世界围棋冠军、职业九段选手李世石,以4:1的总比分获胜。阿尔法围棋程序的工作原理基于下列哪项技术:
量子计算
深度学习
纳米技术
基因编辑
1/4,1/2,5/8,7/10,3/4,( )
14/9
11/14
13/14
17/16


 陕公网安备 61010302000399号
陕公网安备 61010302000399号