甲、乙两个工程队共同完成某项工程需要12天,其中甲单独完成需要20天。现8月15日开始施工,由甲工程队先单独做5天,然后甲、乙两个工程队合作3天,剩下的由乙工程队单独完成,问工程完成的日期是:
9月5日
9月6日
9月7日
9月8日
据2006年人口变动抽样调查,年末浙江省常住人口为4980万人,比上年增长1.67%。其中,男性人口2511.4万人,女性人口2468.6万人,分别占总人口的50.43%和49.57%。全年出生人口50.78万人,出生率为10.29%;死亡人口26.75万人,死亡率为5.42%。
据对全省城乡住户抽样调查,全省城镇居民人均可支配收入18265元,农村居民人均纯收入7335元,分别比上年实际增长10.9%和9.3%。城镇居民人均住房使用面积26.4平方米,比上年末增加0.3平方米;农村居民人均居住面积55.6平方米,比上年末增加0.6平方米。
全年全省参加企业养老保险人数964.4万人,比上年末增加87.6万人;企业实际缴费人数722万人,企业养老保险基金收入318.2亿元,支出192.3亿元,累计结余453.7亿元,比上年末增加125.9亿元,基金支付能力稳定上升,支付能力达26个月。参加失业保险人数504.4万人,比上年末增长13.4%;基本医疗保险参保人数730.6万人,比上年末增长14.2%;工伤保险参保人数604万人,比上年末增长33.3%。
新型社会救助体系进一步深化完善。全省已有城乡低保对象62.9万人,其中城镇8.9万人,月均补助145.5元/人;农村54万人,月均补助72.3元/人。年末全省各种收养性社会福利单位拥有床位10.69万张,收养人员7.56万人。农村“五保”集中供养率92%,城镇“三无”集中供养率98%。现有1500多个乡镇(街道)和2.7万个社区(村)建立了社会救助综合管理服务机构,分别占总数的98.6%和73.4%,社会救助工作人员3.8万名。
已知2005年女性人口约占全省常住人口总数的49.3%,则2005年全省的女性人口约为:
2367万人
2391万人
2415万人
2432万人
按照世界银行的界定,基尼系数反映的是收入或消费支出在不同个人或家庭的分布。世界上大多数国家统计的是收入的分布,并且将收入界定为税后的可支配收入,但也有一些国家统计的是消费支出的分布,比如印度。由于边际消费倾向递减的因素,用消费支出计算的基尼系数会明显低于用收入计算的基尼系数,比如,2005年世界银行公布的印度基尼系数是0.33,但如果用收入指标衡量将超过0.6;反之,如果用消费支出法计算中国的基尼系数,则2005年中国基尼系数将只有0.26。
上述文字意在说明:
印度的基尼系数计算存在问题
目前基尼系数计算指标的差异性影响了各国之间的可比性
使用税后收入计算基尼系数最合理
中国的基尼系数被高估
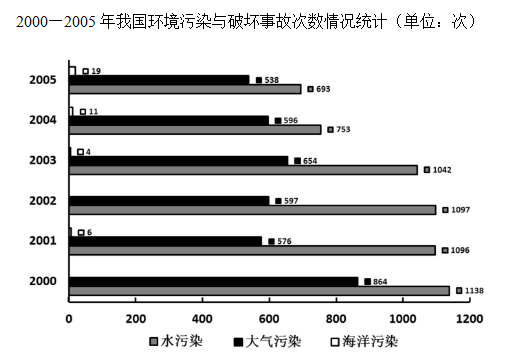
2000年至2005年间,我国水污染次数最多的一年是:
2000年
2001年
2002年
2003年
2018年3月11日,第十三届全国人民代表大会第一次会议审议通过了《中华人民共和国宪法修正案》。
关于这次修宪,下列说法正确的是:
将“健全社会主义法制”写入了《宪法》序言
将坚持“五项原则”修改为坚持“和平发展道路”
增加了“中国共产党领导是中国特色社会主义最本质的特征”
删除了“国家工作人员就职时应当依照法律规定公开进行宪法宣誓”
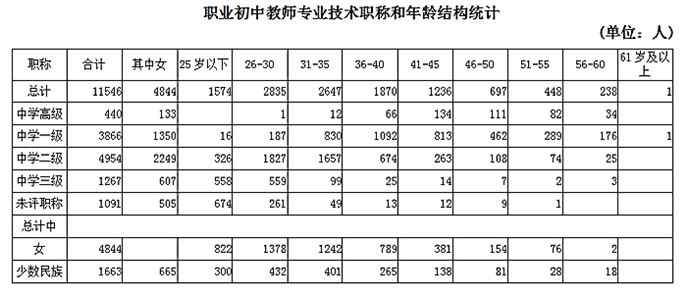
职称为中学二级的男教师占职业初中全体教师总数的比例约为:
38.7%
42.3%
22.9%
23.4%
根据国家卫健委的数据,约有三分之一的中小学生每天户外运动时间不足一小时,超过的中小学生睡眠时间不达标,同时,重压也对青少年的健康造成影响,近视率不断上升,原因主要是家庭作业耗时太长。为此,有教育部门认为,晚上睡个好觉或许对孩子们更重要,在父母同意的情况下,孩子可在指定的睡眠时间后不做尚未完成的作业。但家长们并不感到高兴,他们担心自己的孩子最终只能上低质量的学校。
以下哪项如果为真,最有助于解释家长们的担心:
新规虽可能会减轻学生的作业负担,但现行规则下,大学都是依据高考成绩选择学生
未来将开展人工智能辅助教学,学生们耗费在家庭作业上的时间将大大减少
有研究证明,良好的睡眠能够提高学习效率,有助于提高学习成绩
高校录取机制将进行新的改革,关注学生成绩的同时也会更加重视学生的综合素质
N中学在进行高考免试学生的推荐时,共有甲、乙、丙、丁、戊、己、庚等7位同学入围。
在7人中,有3位同学是女生,4位同学是男生,
有4位同学的年龄为18岁,而另3位同学年龄则为17岁。
已知,甲、丙和戊年龄相同,而乙、庚的年龄则不相同;
乙、丁与己的性别相同,而甲与庚的性别则不相同。
最后,只有一位17岁的女生得到推荐资格。
据此,可以推出获得推荐资格的是:
庚
戊
乙
甲
甲、乙、丙三队进行足球循环赛。已知有下列情况:
根据上表情况,可以得出甲队对丙队的进球数之比是:
3:1
3:2
1:0
0:0
圆周率是一个在数学及物理学领域普遍存在的数学常数。它被定义为圆形之周长与直径之比,是精确计算圆周长、圆面积、球体积等几何形状的关键值。世界上最早计算圆周率数值的是:
中国数学家祖冲之
中国数学家刘徽
印度数学家阿耶波多
古希腊数学家阿基米德

 陕公网安备 61010302000399号
陕公网安备 61010302000399号