2017年9月,党中央、国务院批复的《北京城市总体规划(2016年-2035年)》提出,要构建“一核一主一副,两轴多点一区”的城市空间结构。2020年8月,党中央国务院批复的《首都功能核心区控制性详细规划(街区层面)(2018-2035)》,对未来核心区发展、建设和管理的目标方向、基本依据和具体要求都做了较为详细的规定。至此,首都规划体系的“四梁八柱”已初步形成,首都规划进入新的历史阶段。
《首都功能核心区控制性详细规划(街区层面)(2018-2035)》提出,要全面强化老城空间的整体性,加强九坛八庙保护。关于九坛八庙,下列说法中错误的是:
天坛为明清两代帝王祭天的场所
明清两代帝王每年秋分时在“日坛”祭日
太庙是明清两代皇帝祭奠祖先的家庙
雍和宫先为雍亲王府,后成为藏传佛教寺庙
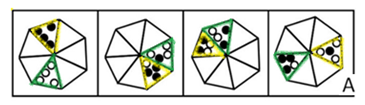
从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:【2010安徽071】

如图所示
如图所示
如图所示
如图所示
从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:【2010安徽069】
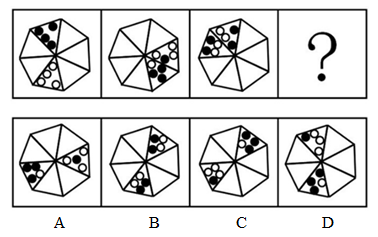
如图所示
如图所示
如图所示
如图所示
从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:【2009安徽073】
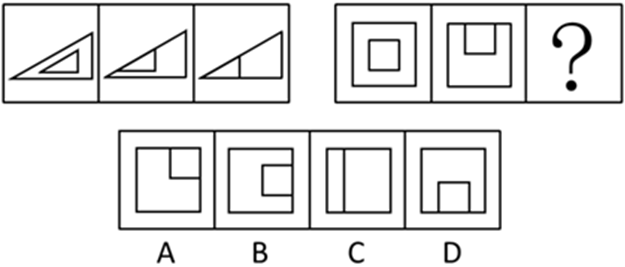
如图所示
如图所示
如图所示
如图所示
从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:【2008安徽055】

如图所示
如图所示
如图所示
如图所示
从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定规律性:【2008安徽054】
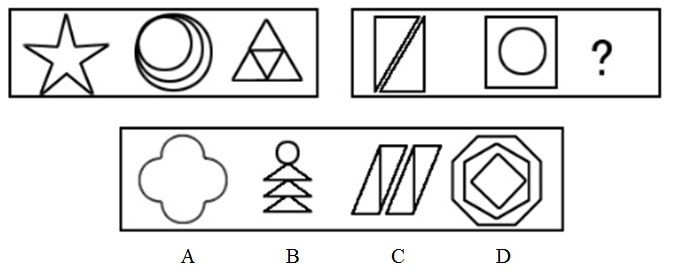
如图所示
如图所示
如图所示
如图所示
老师在课堂上出了18道速算题,规定学生答对一题得6分,答错一题倒扣1分。一位学生全部做完,得了94分,他答对了多少道题?
12
14
16
17
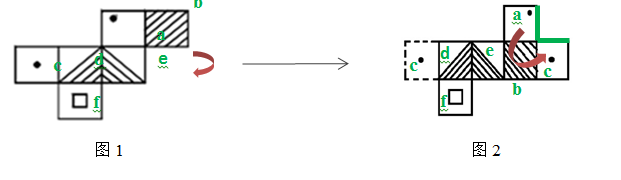
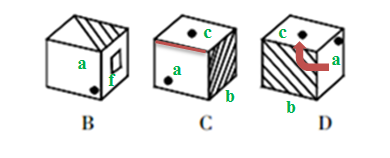
左边给定的是纸盒的外表面,下列哪一项能由它折叠而成:【2013联考/安徽076】
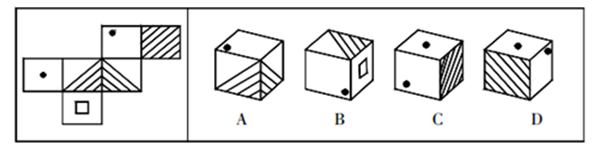
如图所示
如图所示
如图所示
如图所示
我和我在基础物理学界的同事们是爱因斯坦的理性的后继者,乐于自认为我们是在探求美。有些物理方程丑得让人不愿多看一眼,更不用说把它们写下来了。毫无疑问,终极设计者只会用美的方程来设计这个宇宙!我们宣称,如果有两个都可用来描述自然的方程,我们总要选择能激起我们的审美感受的那一个。“让我们先来关心美吧,真用不着我们操心!”这就是基础物理学家们的呼声。
读者也许会把物理看成一个具有精确预言性而不适于审美沉思的科学。其实,审美事实上已经成了当代物理学的驱动力。物理学家已经发现了某些奇妙的东西:大自然在最基础的水平上是按美来设计的。我希望与你们分享的正是这种奇妙的感受。
“美”一词被赋予了一定的内涵。在日常生活中,我们对美的感受是依赖于心理、文化、社会甚至常常是生理等因素的。物理学显然不会关心这一类的美。
自然在她的定律中向物理学家展示的美是一种设计美。因强调几何对称,这种美在一定程度上使我们想到了古典建筑。物理学家在审视自然时所用的美学体系也是从这种朴素的几何确定性中吸取精髓的。请在纸上画出一个圆、一个正方形和一个矩形。快,哪一个图形更能使你愉悦?按古希腊人的观点,多数人大概会选择圆。当然,正方形甚至矩形也不会没有热忱的崇拜者。但存在一个客观的判据,它按圆形、正方形、矩形的次序来排定三种图形的名次,按此次序:圆具有更高的对称性。
或许我不该问哪一个图形更美,而该问哪一个图形的对称性更高。但是,按古希腊人对球形以及它们所构成的天体的完美性的雄辩论述,我还是要继续将对称等同于美。
对称性的精确数学定义涉及到不变性的概念。如果一个几何图形在某些操作下保持不变,就说这个图形在这些操作之下具有不变性。例如,圆在绕它的中心旋转时是不变的。作为一个抽象实体,不管我们把它转17度还是转其它角度,这个圆都不会变。而正方形就不一样,只有绕它的中心转90°、180°、270°和360°时(考虑对几何图形的影响时,转360°和转0°或不转是等价的)才保持不变。矩形的对称性比正方形的还要低,只有绕它的中心转180°和360°时才保持不变。
基础物理学家选择探求的美是:
日常生活中依赖心理和文化的直觉认识
物理学家在审视自然时所用的美学体系是古希腊人的古典建筑美
图形的对称性
激起审美感受的描述自然的方程
下列现象与物理效应之间无法对应的一组是:
墙内开花墙外香-扩散现象
杯弓蛇影-折射现象
镜中花,水中月-平面镜成像
立竿见影-光沿直线传播现象
 陕公网安备 61010302000399号
陕公网安备 61010302000399号