一声巨响、凄厉的尖叫······被吓得呆若木鸡,一动不动的体验,你有吗?再次听到类似声音,即使时隔多年,恐惧也会被重新勾起。大脑是如何存储恐惧记忆的?
动物对于恐惧的记忆,一部分是先天的,比如老鼠闻到猫的气味就会害怕,另一部分则是习得的,与巴甫洛夫著名的条件反射实验差不多,当一种声音与恐惧联系在一起,只要再次听到这种声音,动物就会重新陷入惊恐之中。
很多恐惧记忆的形成,与大脑中附着在海马末端的杏仁核息息相关。这是一个产生、识别和调节情绪,并控制学习和记忆的脑部组织。原先,科学家认为,小鼠听觉恐惧的信息会从大脑的听觉感觉区流向杏仁核的侧杏仁核,再通往下游直接控制运动的区域,由此产生恐惧反应,而从杏仁核回到感觉皮层的投射,只有在猕猴等灵长类动物中存在。可是上海有位年轻的女研究员最近在浏览小鼠大脑连接图谱时突然发现,小鼠听觉皮层也有来自侧杏仁核的投射,于是她就和另一位女博士一起“追踪”了下去。
这一追,收获巨大。她们研究发现,从侧杏仁核投射回大脑初级听觉皮层的这个神经回路一旦被抑制,小鼠就不那么害怕原先非常恐惧的声音。这说明,假如我们可以在人脑中找到对应的通路,那么我们就可能通过调节这个通路,减轻焦虑症和创伤后应激障碍等疾病。这一基础研究的发现,将为未来脑疾病的治疗提供新的线索,“目前药物治疗脑疾病效果并不理想,而生理、物理刺激和干预,可能取得更好的效果。”
不过,更有意义的是,这两位年轻的女科学家发现了成年大脑存储恐惧记忆的模式——这是科学家从来没发现过的。
与电脑有一个像集中存储数据的硬盘不同,大脑是将信息存储在以突触为基本单元的神经网络中。突触是神经元之间的连接点,大脑中有数以千亿计的神经元,每个神经元都与上千个同伴相连接,它们之间传递信号,就是通过突触完成的。而突触会不断变化,形态、数目以及连接方式,都会随着学习和记忆改变。通过荧光标记,她们发现,侧杏仁核-听皮层的突触在经过恐惧训练后,明显增多了。通过观察发现,98%以上新形成的突触都遵循“部分新增”的规律。也就是说,这些新突触往往由旧有突触“改造”而来,这种形成新突触的方法,不仅可以节省空间、细胞能量,还可节省“建材”——结构蛋白的数量。她们在所有与学习有关或无关的突触变化中,都看到了这个现象,所以这可能是成年动物大脑中突触形成的普遍规律。目前,这项极具价值的研究通过脑科学卓越中心的合作机制,已有北京的人工智能科学家基于这一发现,开始研发新的人工智能存储网络。
下列说法不符合原文意思的是:
附着在海马末端的杏仁核是一个生产、识别和调节情绪,并控制学习和记忆的脑部组织,具有传递恐惧信息的作用
老鼠闻到猫的气味就会害怕,说明动物对于恐惧的记忆是先天的
当一种声音让人产生恐惧,再次听到这种声音,就会重新陷入惊恐,这种现象可以用巴甫洛夫的条件反射学说来解释
在听觉恐惧记忆中起重要作用的侧杏仁-听觉皮层投射通路,不仅仅在猕猴等灵长类动物中存在
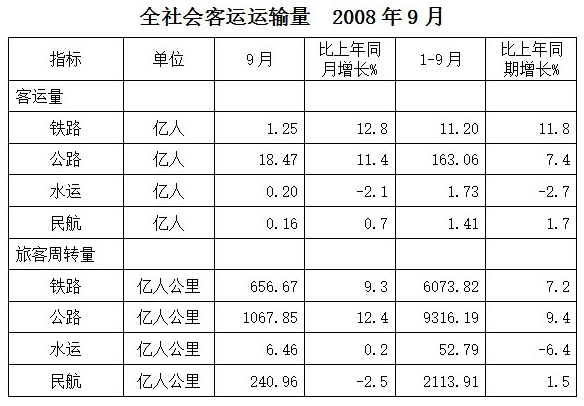
2008年1-9月,公路在旅客周转量比重比铁路多多少个百分点:
2.2
3.1
18.5
20.9
据世界卫生组织统计,每年有1200万人过早地被心血管、脑血管疾病夺去了生命,心血管、脑血管疾病的死亡率为各种疾病死亡率之首,而“中风”则是心血管、脑血管疾病的元凶。如果用“养神3分钟”自我治疗预防,每年可使全世界少死300万人,一年也可使我国少死60万人,因为“中风”多发生在夜间,最危险时刻是醒来的“一刹那”。但有绝招可防这“一刹那”,即在苏醒时,养神3分钟,定可逢凶化吉。
本文主要谈的是什么病:
中风
高血压
心脏病
脑血管病
地膜覆盖∶增温保水
田间管理∶霜冻虫害
临床试验∶不良反应
天气预报∶卫星云图
整顿市场∶净化风气
甲、乙两人从环形跑道的A点同时出发背向而行,6分钟后两人第一次相遇,相遇后两人的速度各增加10米每分钟,5分钟后两人第二次相遇。问环形跑道的长度为多少米?
600
500
400
300
素数是指只含有两个因子的自然数(即只能被自身和1整除),孪生素数是指两个相差为2的素数。比如,3和5,17和19等。所谓的孪生素数猜想,是由希腊数学家欧几里得提出的,意思是存在着无穷对孪生素数。该论题一直未得到证明。近期,美国一位华人讲师的最新研究表明,虽然还无法证明存在无穷多个之差为2的素数对,但存在无数多个之差小于7000万的素数对。有关方面认为,如果这个结果成立,那么将是数论发展的一项重大突破。
以下哪项如果为真,最能支持有关方面的观点:
7000万这个数字很大,离孪生素数猜想给出的2还有很大距离
这是第一次有人正式证明存在无穷多组间距小于定值的素数对
关于孪生素数猜想的证明需要一个漫长的、逐步推进的过程
这位华人讲师长期从事数学领域的相关教学和科研工作
一个正方体木块放在桌子上,每一面都有一个数,位于对面两个数的和都等于13,小张能看到顶面和两个侧面,看到的三个数和为18;小李能看到顶面和另外两个侧面,看到的三个数的和为24,那么贴着桌子的这一面的数是多少:
4
5
6
7
甲、乙、丙三个小朋友中任意两人身高的平均数加上另一个小朋友的身高,分别为258cm,238cm,230cm,则这三个小朋友的平均身高是()cm。
118
120
121
122
一个办公室有2男3女共5个职员,从中随机挑选出2个人参加培训,那么至少有一个男职员参加培训的可能性有多大:
60%
70%
75%
80%
某企业4个分公司今年的销售额之和是去年的1.2倍。其中,甲分公司的销售额增长了50%,乙分公司的销售额与去年相同,丙和丁分公司的销售额均增长了25%。已知去年甲、丙、丁三个分公司的销售额之比为2:3:5,则乙分公司今年的销售额占4个分公司总量的:
![]()
![]()
![]()
![]()

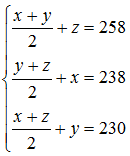 ,三式相加可得:2(x+y+z)=726;
,三式相加可得:2(x+y+z)=726; 陕公网安备 61010302000399号
陕公网安备 61010302000399号