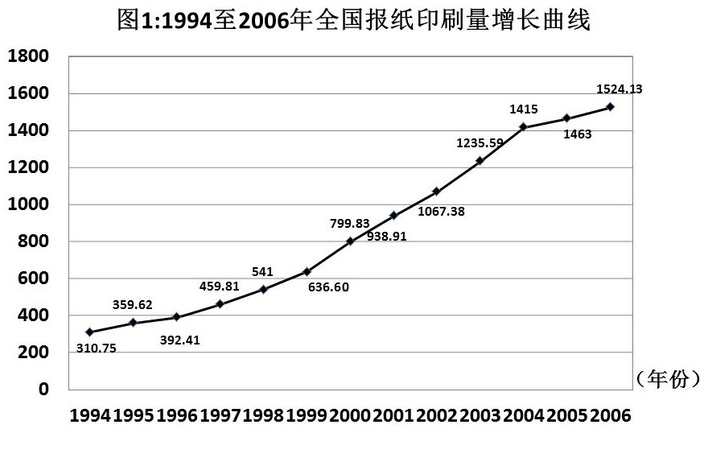
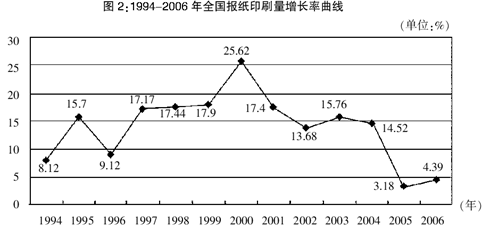
在1994-2006年间,全国报纸印刷总量持续增长。
以2004年为例,年印刷量在10亿对开张以上的企业有30家,其中印刷量增长的企业占90%,而且全部增长5%以上,增长率达两位数的企业占66.67%。年印刷量在5亿至10亿对开张之间的企业有26家,其中印刷量增长的有25家,增长率达到两位数的有19家。
到了2005年,年印刷量在10亿对开张以上的企业有29家,其中印刷量增长的有17家,增长5%以上的有11家,而保持两位数增长的有8家。印刷量减少的企业有11家。年印刷量在5亿至10亿对开张之间的企业有31家,其中印刷量增长的有20家,增长5%以上的有16家,保持两位数增长的有13家。印刷量减少的企业有10家。
再看2006年,年印刷量在10亿对开张以上的企业有31家,其中印刷量增长的有19家,增长5%以上的有14家,保持两位数增长的有10家。印刷量减少的企业有11家。年印刷量在5亿至10亿对开张之间的企业有28家,其中印刷量增长的有20家,增长5%以上的有14家,保持两位数增长的有7家。印刷量减少的企业有8家。
2006年,年印刷量在10亿对开张以上的企业中,印刷量增长5%以上且低于10%的企业有多少家:
3
4
5
8
甲、乙、丙、丁、戊5支足球队进行小组单循环赛。比赛规定:每队胜一场得3分,平一场得1分,负一场得0分;积分前两名出线。比赛结束后发现,没有积分相同的球队,乙队胜了3场,另一场负于甲队。
根据以上信息,可得出以下哪项:
甲队一定出线
乙队一定出线
丙队一定出线
戊队一定出线
10名志愿者准备将村民们刚采摘的一堆西瓜平均装上甲、乙两辆运输车,西瓜总数正巧满足每个村民采摘的西瓜个数都等于该村村民数。志愿者们先每人抱一个西瓜放到甲车上,然后每人抱一个西瓜放到乙车上,依次轮流进行,直到所剩西瓜少到容易清点时再平分。当最后1次把10个西瓜放到甲车后,发现所剩西瓜不足10个,于是,不得不从甲车抱出几个与所剩西瓜一起放到乙车上,此时刚好两车所装西瓜一样多。问最后从甲车拿出几个西瓜?
1
2
3
4
某工程由10名工人承担,5天后,为了要提前10天完成任务,需增加4名工人,那按计划完成该工程需要()天。(假设所有工人的工作效率相同)
35
40
65
80
某乒乓球俱乐部决定举办一场所有会员间的循环赛,经俱乐部委员会计算,所需比赛场数刚刚超过2000场,即使省略掉委员会委员们之间的比赛,场数仍有2001场,那么这个乒乓球俱乐部有多少委员:
6
7
8
9
规定如下运算法则:X△Y=X-Y÷2,根据该运算法则,(7△10)△4的值为:
3
2
1
0
人民币的面值中只有1、2、5、10等数值,而缺乏3、4、6、7、8、9等数值。主要是因为:
这几个数值都是整数
这几个数值容易辨认,而其他数字容易搞混
这几个数是重要的数,用其通过计算可得其他数值
这几个数值没有特别意义,只是根据人们的习惯确定的
甲体育场是乙市的地标性建筑,经常举行大型体育赛事或文娱活动。该体育场除了平时正常使用的出入口,还有5个平时不开放的、仅供紧急情况下使用的出入口。这些紧急出入口的启用需要遵守以下规则:
Ⅰ.如果启用1号门,那么必须同时启用2号门并且关闭5号门
Ⅱ.只有关闭4号门,才能启用2号门或者5号门
Ⅲ.同时关闭3号门和4号门是不允许的
如果要启用1号门,同时还要启用:
2号门和4号门
3号门和5号门
2号门和3号门
4号门和5号门
两支篮球队打一个系列赛,三场两胜制,第一场和第三场在甲队的主场,第二场在乙队的主场。已知甲队主场赢球概率为0.7,客场赢球概率为0.5。问甲队赢得这个系列赛的概率为多少:
0.3
0.595
0.7
0.795
甲、乙、丙、丁、戊5支足球队进小组单循比赛。比赛规定,每队胜一场得3分,平一场得1分,负一场得0分;积分前两名出线。比赛结束后发现,没有积分相同的球队,乙队只胜了3场,丙队、丁队均只胜了两场。
根据以上陈述,可以得出以下哪项:
甲队一定出线
丙队一定出线
丁队一定没出线
戊队一定没出线

 陕公网安备 61010302000399号
陕公网安备 61010302000399号