上世纪70年代,湖南长沙马王堆汉墓出土了12万字以上的帛书,其中有一部失传已久的《相马经》,是我国动物学、畜牧学的重要文献。春秋战国时期,由于已从车战演变到骑兵作战,马的身价愈来愈高。传说中的相马专家是伯乐,事实上,这类专家数量众多,《吕氏春秋》就提到十个相马家,《史记》也提到“以相马立名天下”的人士,这些都可以证明古人对相马的重视。
下列说法与原文相符的是:
相马技术的发展使得车战逐渐被淘汰
《相马经》是伯乐所撰写的相马学专著
相马术的出现推动了古代动物学的发展
相马师这一职业早在汉代以前就已经出现
商品生产越发达,社会化程度越高,人们越是相互依赖。商品交换的规模越大,频率越高,法律规则的数量就越多,覆盖面就越广,由商品经济形态所需要和决定的法律规则具有权利本位性,权利和义务的对等性、对象的普遍性及确定性、连续性和稳定性等优良品格,这同自然经济形态和产品经济形态所需要、并由它们各自所决定的法律规则具有质的根本区别。
对这段文字的主旨概括最准确的是:
法治观念强于人治,有利于社会关系的稳定
自然经济产生的法律规则具有权利和义务的对等性
法治观念与商品经济关系密切,法治及其观念的形成是以商品经济发展为基础的
产品经济形态产生的对象的普及性及确定性,是一种最完善的法制
某企业秉持人才为上的理念,一直致力于专业技术人才队伍建设,十年来,该企业招聘的大部分机械工人来自甲职业技术学院,今年招聘的机械工人总数明显增加,但从该学院招聘的机械工人数量却大幅减少,而且招进来的很多人没有经过职业技术学院系统的学习。
以下哪项如果为真,最能解释该企业今年招聘情况的变化?
该企业增设了技术培训部门,以培训新招聘的机械工人
三年前,该企业的管理层进行了重大重组,决定推广AI的应用
从去年开始,权威的职业技术学院排行榜上,甲学院落后于乙学院
很多没有上过职业技术学院的工人很有才华,只是没有机会上学
某单位前台有两个窗口,办理业务的人员要先到1号窗口审核资料,审核通过的才可以到2号窗口缴费。已知平均一份资料的审核时间为1.5分钟,且审核通过率仅有![]() ,而一份资料的缴费时间仅为50秒。假设前台共有10名工作人员,且各窗口的人员数量固定,则1号窗口应安排多少人,才能使得前台运作效率最高:
,而一份资料的缴费时间仅为50秒。假设前台共有10名工作人员,且各窗口的人员数量固定,则1号窗口应安排多少人,才能使得前台运作效率最高:
9
8
7
6
人口密度是单位面积土地上居住的人口数,它是表示世界各地人口的密集程度的指标。但人口密度只反映人口与土地面积的一般数量关系,不能体现单位面积土地上的人口成分,也不能体现人口与实际供养他的土地面积的关系。为了弥补这些缺陷,出现了一些新的补充性密度指标,如生理密度、农业密度等,而以面积计算的人口密度称为人口的数学密度。
这段文字意在说明:
人口密度含义演变的原因
补充性密度指标的产生过程
人口密度的具体表现形式
土地面积和人口成分的关系
4艘轮船负责6个码头之间的货物调配任务,已知这6个码头所需装卸工的数量分别为12人、10人、6人、8人、3人、9人,现在让一部分装卸工跟随轮船移动,而不是在各自的码头等待轮船到来后才开始工作,这样一来,可以使得6个码头所需装卸工的总数减少,则在不影响任务的前提下,所需装卸工的最少人数为多少人:
48
39
45
31
我国全面建设社会主义现代化国家的进程分为两个阶段,2035年的目标是基本实现社会主义现代化,2050年的目标是建成富强民主文明和谐美丽的社会主义现代化强国。
关于这两个阶段目标的特点,下列理解正确的是:
①紧扣我国社会主要矛盾的变化
②突出了以人民为中心的现代化
③设定了增长的数量指标和质量指标
④突出了“四个全面”战略布局的目标要求
①②③
①③④
①②④
①②③④
我国已进入快速老龄化的发展阶段,如何养老是无可回避的大问题。“养儿防老”是我国传统养老方式的基本特征。在儒家思想影响下,家庭养老观念根深蒂固。相当长的时期内,人们都是通过生养子女来解决养老问题的。不过,未富先老、子女数量减少等各种因素正在冲击这一传统模式,致使家庭养老功能不断弱化。必须提高社会养老能力,才能适应加速到来的老龄化社会的要求。
这段文字意在强调:
老龄化加速到来将引发养老革命
家庭养老功能逐渐退居次要地位
满足养老需求将是巨大的社会难题
老龄化趋势要求提升社会养老能力
澳大利亚研究者研制出一种计算机芯片,他们在一种失明者的大脑视觉皮层中植入该计算机芯片,并将芯片与一副眼镜建立无线连接,借助该眼镜,失明者可看到外界的事物。芯片处理信息需要持续的电量来提供动力,因而大脑中需要植入相当数量的电极。据此,研究者认为这种计算机芯片是能够帮助失明者恢复视觉能力的。
以下哪项是研究者作出上述判断所需的前提:
已有研究表明,在失明者大脑中植入计算机芯片对人体无不良影响
与植入眼睛的人造视网膜相比,植入大脑的芯片恢复视力的效果更好
失明者大脑中植入芯片后,无需经过培训即可使用该眼镜片适应其视觉效果
芯片处理信息的电能只能由电极提供,电极数量越多,提供的电量越足
有人曾经对城市所拥有的加油站的数量进行过统计,发现加油站总数的增长和城市人口总数的增长之间不是简单的线性关系,前者是后者的0.77次方。例如,某城市的人口总数增加10倍,其加油站总数只增加到10的0.77次方倍,也就是5.9倍;如果人口总数增加100倍,那么加油站总数就会增加到100的0.77次方倍,也就是34.7倍。
由此,可以推知:
加油站数量的增长速度可能满足不了成倍增长的城市人口的需求
若一个城市的出生率小于死亡率,则其加油站的总数不会增加
城市人口规模越大,加油站数量增长幅度越小
城市人口和总油耗之间存在非线性关系

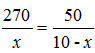 ,解得x=8.43,因此1号窗口应安排8人。
,解得x=8.43,因此1号窗口应安排8人。 陕公网安备 61010302000399号
陕公网安备 61010302000399号