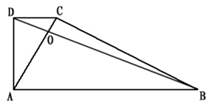
如图，在四边形ABCD中，AC与BD相交于O点，∠ADC=∠BAD=90°，△COD的面积为1.5，且CD=3，AD=5，那么△BOC的面积为：
4
5
6
7.5
定义：①爬山法：指经过评价当前的问题状态后，限于条件，不是去缩小，而是去增加这一状态与目标状态的差异，经过迂回前进，最终达到解决问题的总目标。
②降维法：指在解决问题过程中，根据问题需要，利用特定观察角度降低维数，化繁为简，化面为点，从而使研究的对象更为直观、求解过程更为简捷的方法。
③陡度法：指在解决问题过程中，选好几个点，分别找准特点，然后对差异悬殊的进行比照，看看哪一个最“陡”，从而使研究对象的特点更为显著的方法。典型例证：
（1）以前，小张天天游泳，他的颈椎病没有好，后来，他天天爬山，结果颈椎病好了。
（2）某公司以前实行过程管理，现在该公司实行目标管理。
（3）某化工厂为解决问题，先选了一个角度做了两个实验，随后立刻转到相关的另一个角度又做了两个实验。发现第二次的一个实验特好，而第一次的一个实验特差。在这种情况下再把特好、特差的合起来做了一个试验，结果终于发现了问题的症结所在。
上述典型例证与定义存在对应关系的数目有：
0个
1个
2个
3个
一个人有两个耳朵，能听话；两只眼睛，能看东西；两个鼻孔，能闻味。听话，能听正面的，也能听反面的；看东西，能看白的，也能看黑的；闻气味，能闻香的，也能闻臭味的，所以，_______________。
横线上为这段文字所填写的结论性语句是：
人体构造也是符合美学原理
人的机能也是合乎辩证规律的
面对纷繁复杂的世界，我们必须善于辨别
万事万物都具有两面性的特点
某地市区有一个长方形广场，其面积为1600平方米。由此可知，这个广场的周长至少有：
160米
200米
240米
320米
米时，周长最少。
某商场促销，晚上八点以后全场商品在原来折扣基础上再打9.5折，付款时满400元再减100元，已知某鞋柜全场8.5折，某人晚上九点多去该鞋柜买了一双鞋，花了384.5元，问这双鞋的原价为多少钱：
550
600
650
700
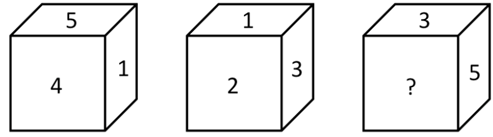
一个正方六面体上标有数字1、2、3、4、5、6，根据下图，“？”处的数字为：
1
2
4
6
有一段路，原计划每天修0.48千米，15天可完成，因为时间紧急，每天多修0.12千米，则可提前( )天完成修路。
12
8
4
3
甲、乙两人分别从A、B两地同时出发，相向而行，匀速前进。以原速度前进，4小时相遇；如果各自每小时比原计划少走1千米，5小时相遇。则甲乙两地的距离是：
40千米
20千米
30千米
10千米
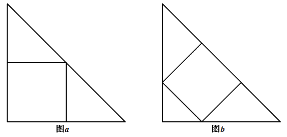
，化简得a+b=10，因此A、B两地的距离是10×4=40千米。在大小相等的两个等腰直角三角形中，按不同的方式各内接一个正方形（如图a、b所示）。如果图b中的内接正方形的面积是144，那么图a中的内接正方形的面积是多少：
225
162
128
98
，原等腰直角三角形的斜边长为12×3=36，直角边长为
；
，其内接正方形的边长为
，图A中正方形的面积为
。小张早上起床的时候，发现挂钟电池没电已经停止了，他把挂钟换好电池，但未来得及调整时间就匆忙出门上班了，出门前挂钟显示时间是5点25分。小张赶到单位时，刚好是8点整。中午12点小张从单位返回家中吃饭，12点半进门。假设小张上下班路上花费时间相等，则小张进门时家里挂钟显示时间为：
9点25分
9点55分
10点25分
10点55分
陕公网安备 61010302000399号