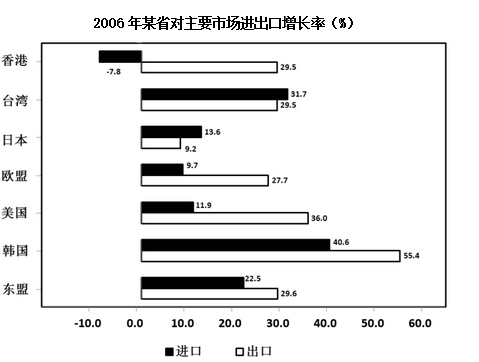
2006年某省全年进出口总额为1391.5亿美元,比上年增长29.6%,其中进口382.5亿美元,增长25.1%,出口1009亿美元,增长31.4%。对主要市场的出口均保持较快增长,韩国和台湾成为2006年该省进口增长较快的国家和地区。
2006年全省新批外商直接投资项目3583个,比上年增加187个,合同外资和实际到位外资分别为191亿元和88.9亿美元,分别增长18.5%和15.1%。第三产业利用外资继续保持良好势头,合同外资47.9亿美元,实际外资19.6亿美元,分别增长25.9%和33.6%,分别占外资总额的25.1%和22.1%,比重分别提高1.5和3.1个百分点。
2006年全年对外承包工程、对外劳务合作、对外设计咨询完成营业额20.3亿美元,比上年增长15.8%。批准境外投资项目425个,总投资3.9亿美元,其中中方投资3.0亿美元,总投资和中方投资分别增长99.6%和79.1%。
2006年该省对主要市场进口增长率最低与最高的国家和地区相差的百分点为:
32.8
35.2
46.2
48.4
某甜品店出售一种规则球形的甜品,该甜品由内部中空的球形面皮(每立方厘米成本0.4元),和实心的芝士球(每立方厘米成本1元)组成,无论甜品大小规格如何,其中的芝士球半径始终为甜品半径的四分之三,已知制作半径为1厘米的该甜品成本约为2.73元那么要制作半径为2厘米的该甜品,成本约为:
5.46元
7.45元
14.92元
21.88元
已知![]() ,A、B为自然数,且A≥B,那么A有几个不同的值:
,A、B为自然数,且A≥B,那么A有几个不同的值:
2
3
4
5
2022年1月末,我国人民币贷款余额196.65万亿元,同比增长11.5%,增速分别比上月末和上年同期低0.1个和1.2个百分点。1月份我国人民币贷款增加3.98万亿元,同比多增3944亿元。分部门看,住户贷款增加8430亿元;企(事)业单位贷款增加3.36万亿元,其中,短期贷款增加1.01万亿元,中长期贷款增加2.1万亿元,票据融资增加1788亿元。2022年1月末,我国外币贷款余额9308亿美元,同比增长2%。1月份外币贷款增加181亿美元,同比少增269亿美元。
2022年1月末,我国人民币存款余额236.07万亿元,同比增长9.2%,增速分别比上月末和上年同期低0.1个和1.2个百分点,1月份人民币存款增加3.83万亿元,同比多增2627亿元,其中,住户存款增加5.41万亿元,非金融企业存款减少1.4万亿元,财政性存款增加5849亿元。1月末,外币存款余额1.02万亿美元,同比增长9%。1月份外币存款增加272亿美元,同比少增228亿美元。
2022年1月份,我国银行间人民币市场以拆借、现券和回购方式合计日均成交6.31万亿元,日均成交同比增长18%。其中,同业拆借日均成交同比增长9.3%,现券日均成交同比增长22.9%,质押式回购日均成交同比增长18.2%。
2022年1月份,我国企(事)业单位贷款增加额占人民币贷款增加额的比重比住户贷款所占比重高约多少个百分点?
30
40
50
60
大约公元前450年,古希腊哲学家阿那克萨哥拉提出一个有趣的问题:只用直尺和圆规,能否作出一个与给定圆面积相等的正方形?这个看似简单的“化圆为方”问题成为尺规作图领域的经典题目,在此后的两千多年中,许多数学家尝试解答却都未能成功。这个问题之所以难以解答,在于它不仅是一个几何学问题,还是一个代数学问题。在尺规作图问题中,给定若干角度或线段长度,实质是给出了若干实数;只用直尺和圆规作图这条规则,保证了作出的角度或线段的长度,是给定实数的和、差、积、商、平方根的组合。因此每个尺规作图问题,其实都对应着一个代数问题。
关于“化圆为方”问题,文中没有谈到:
提出问题的具体背景
关于问题实质的分析
问题难以解答的原因
对该问题的大体描述
一电信公司在每晚九点到次日早七点以及周六、周日全天实行长话半价收费。请问该电信公司在一周内共有多少个小时实行长话半价收费:
114
84
98
91
小吴到商店买布。有两种同样长的布料,小吴买了第一种布料25米,买了第二种布料12米。小吴买完后,第一种布料剩下的长度是第二种布料剩下的长度的一半。那么这两种布料原来共有多少米:
26
38
72
76
一个由4个数字(0-9之间的整数)组成的密码,每连续两位都不相同,问任意猜一个符合该规律的数字组合,猜中密码的概率为:
![]()
![]()
![]()
![]()
如下图所示,甲和乙在面积为54π平方米的半圆形游泳池内游泳,他们分别从位置A和B同时出发,沿直线同时游到位置C。若甲的速度为乙的2倍,则原来甲、乙两人相距:

![]() 米
米
15米
![]() 米
米
18米
有两只相同的大桶和一只空杯子,甲桶装牛奶,乙桶装糖水,先从甲桶内取出一杯牛奶倒入乙桶,再从乙桶取出一杯糖水和牛奶的混合倒入甲桶,问,此时甲桶内的糖水多还是乙桶内的牛奶多:
无法判定
甲桶糖水多
乙桶牛奶多
一样多

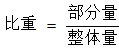 ,则有我国企(事)业单位贷款增加额占人民币贷款增加额的比重比住户贷款所占比重高
,则有我国企(事)业单位贷款增加额占人民币贷款增加额的比重比住户贷款所占比重高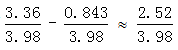 。
。 陕公网安备 61010302000399号
陕公网安备 61010302000399号