一个正六边形,边长为50米,一个人从正六边形的一个角点出发沿边长跑步,跑了500米后,问此人与出发点的直线距离为多少米?
100
![]()
![]()
![]()
![]()
![]()
![]()
![]()
自行车运动员在400米长的环形跑道上骑行了两圈,他前一半时间的平均速度是6米/秒,后一半时间的平均速度是10米/秒,问他第一圈用时为多少秒:
50
60
70
80
小明从A地出发,需要先走一段平路,再爬一段上坡路才能到达B地,到达B地后,他停留一小时后按原路返回A地。小明走平地的速度为16/3千米/小时,上坡速度为4千米/小时,下坡速度为8千米/小时。小明从出发到返回共用7小时,则A、B两地的距离为多少千米:
10
12
15
16
18
24
30
无法计算
某圆形跑道长为400米,甲从跑道上A点以6米/秒的速度顺时针跑步前行。乙在A点对应直径的另一端B点同时以5米/秒的速度逆时针跑步前行,问在14分钟内,他们共相遇了多少次?
22
23
24
25
做同一种零件,赵师傅3小时做15个,钱师傅4小时做21个,孙师傅5小时做27个,李师傅6小时做31个,则( )的工作效率最高。
赵师傅
钱师傅
孙师傅
李师傅
一位管理者让几位员工从皱纹纸带上各裁下一段30厘米的纸带,只能用目测,不能用量具测量。然后,又要求每一位听讲者裁150厘米和600厘米长的纸带各一段。大家裁完后,这位管理者掏出卷尺,仔细地测量一条条纸带并公布结果:30厘米一组,平均误差不到6%;150厘米一组,平均误差上升到11%;600厘米一组,平均误差高达19%,个别的相差100多厘米。
由此推出的是:
目标越小、越集中,越容易接近目标
目标越大、越宽泛,越不容易偏离目标
目标大小适中,最容易接近既定目标
目标大小与接近目标的程度无关
某地打算在绿地上建两个圆形花坛,如下图所示,大圆的直径为6米,小圆的直径为2米,修建期间暂时在外围设置围栏。已知围栏呈矩形,大圆与围栏的三条边相切,小圆与围栏的两条边相切,且两圆相切,那么矩形围栏的面积是多少平方米?

![]()
![]()
![]()
![]()
甲、乙、丙三人沿着长为500米,宽为250米的长方形场地跑步,三人以2:1:3的速度之比匀速顺时针跑步,当甲开跑时乙刚跑完1/3圈,丙开跑时甲跑了100米。问当乙跑完2圈时,甲与丙的位置关系如何?
丙领先甲3000米
丙领先甲2900米
丙领先甲2450米
丙领先甲2350米
一块长方形土地的周长为260米,面积为3600平方米。将该土地划分成边长10米的小正方形土地。现从中选取3块,使得任意两块既不同行也不同列。问有多少种不同的选取方式?
不到200种
200—400种
400—800种
超过800种
某水库每天的上游来水量是10万立方米。5月1日水库向周边供水7万立方米,在5月15日午夜降雨之前,每日的供水量都比上一日多2万立方米。问该水库5月1日零时的库存至少要为多少万立方米,才能保证在降雨之前对周边充足的水供应:
143
150
165
185


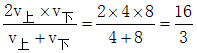 千米/小时;
千米/小时;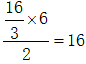 千米。
千米。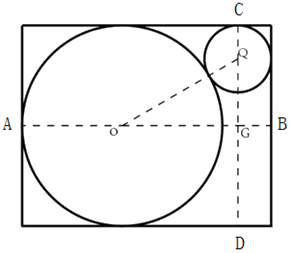
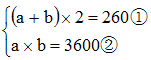 ;
; 。
。 陕公网安备 61010302000399号
陕公网安备 61010302000399号