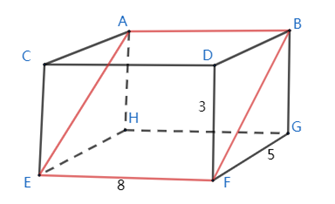
沿一个平面将长、宽和高分别为8、5和3厘米的长方体切割为两部分,问两部分的表面积之和最大是多少平方厘米:
206
238
![]()
![]()
如下图所示,一个小正方体的表面积为64平方厘米,则几何物体甲垒放成几何物体乙后,物体甲与物体乙表面积之比为:
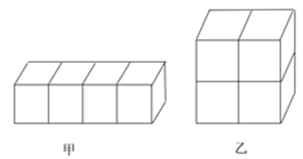
3:2
4:3
8:7
9:8
一只闹钟的秒针顶点距离表盘圆心4厘米,分针顶点距离表盘圆心3厘米。小王烧开一壶水的时间内,秒针顶点累计移动了40π厘米。那么这一时间段内,分针顶点与表盘圆心的连线扫过的扇形面积为多少平方厘米?
0.5π
0.75π
π
1.5π
一个箱子的底部由5块正方形纸板ABCDE和1块长方形纸板F拼接而成(如图所示),已知A、B两块纸板的面积比是1:16,假设A纸板的边长为2厘米,则该箱子底部的面积为( )平方厘米。
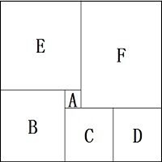
200
320
360
420
一个长方体木块恰好能切割成三个正方体木块,三个正方体木块表面积之和比原来的长方体木块的表面积增加了64平方厘米。则长方体木块的体积为()立方厘米。
128
192
256
512
将一个8厘米×8厘米×1厘米的白色长方体木块的外表面涂上黑色颜料,然后将其切成64个棱长1厘米的小正方体,再用这些小正方体堆成棱长4厘米的大正方体,且使黑色的面向外露的面积要尽量大,问大正方体的表面上有多少平方厘米是黑色的:
84
88
92
96
有红、黄、蓝三种颜色的木棍若干根,所有木棍的长度都是整数厘米,且同一颜色的木棍长度也相同。已知用两红两黄、两红两蓝和两黄两蓝的木棍拼成的长方形,面积分别为20,28和35平方厘米。问蓝色木棍的长度是多少厘米?
8
7
5
4
某加工厂要将一个表面积为384平方厘米的正方体金属原材料切割成体积为8立方厘米的小正方体半成品,如果不计损失,这样的小正方体可以加工的个数为
64
36
27
16
如下图所示,正方形ABCD的边长是14cm,其中,BE=CE=7cm。如果点P以2cm/s的速度沿着边线CD从点C出发到点D,那么△AEP的面积将以每秒多少平方厘米的速度增加:

7
8
9
10
土质房屋的墙壁底部有一个三棱柱体的孔,其纵截面ABC如下图所示。房主用一个纵截面为三角形的木楔塞住这个孔。为了塞紧孔洞,他用锤子敲击木楔,使木楔移动了4厘米(CD)且其底部EF与孔洞表面BG重合,此时孔的高度增加了3厘米(AG)。已知木楔底部EF高8厘米,问孔的纵截面积增加了多少平方厘米?

26
30
32
36



 陕公网安备 61010302000399号
陕公网安备 61010302000399号