应该清醒地认识到,目前房地产市场最大的矛盾不是供需之间的矛盾,而是百姓囊中羞涩与房价不断上涨之间的矛盾。而这一问题产生的根源就在于房子被当作奇货可居、有利可图的商品,被房产商和手有余钱的业主一而再再而三地热炒。于是我们看到一些房产商宁愿把房子成片闲置也不愿平价或降价出售;某些富有的业主拥有两三套,甚至十数套房产,而大量炒房团也应运而生。
以下最能加强上述结论的是:
经济学家近来十分关注炒房对房价上涨的影响作用
在一些内陆地区,未发生炒房现象,房价比较平稳
在一些经济发达的地区,炒房现象虽不突出,但房价仍然居高不下
一些地区拟对拥有多套房者开征土地使用费,可以有效地抑制虚假的住房需求
五人——J、K、L、M和O聚在一起玩一种叫“三人玩”的游戏。游戏的每一圈只能三个人玩。下列是所有的规则,它将影响到每圈游戏参加者的顺序和玩的圈数:
①没有人可以连续玩三圈;
②没有人可以连续两圈不玩;
③每个人都必须玩三圈。
如果J、L和M玩第一圈,而K、M和O玩第二圈,下列哪一位一定玩第四圈:
J
K
L
M
民政部每年公布的结婚率与离婚率,实际上是粗结婚率和粗离婚率,即以结(离)婚对数除以当期平均人口数。这两个指标数据容易获得,计算简便,能够反映出一定时期内人口婚姻事件的发生频率。但是,______________________,因而计算结果会受到人口年龄结构的影响。如果非适婚年龄的人口比重不断增加,那么即使适婚年龄人口中的结婚水平和离婚水平没有发生变化,也会使粗结婚率和粗离婚率呈现出下降的趋势。
填入画横线部分最恰当的一项是:
指标计算时未考虑人口变动抽样调查数据
这种指标并不能反映人口真实的婚姻状况
婚姻事件只在一定年龄范围内的人口中发生
这种计算方法并未排除当期非适婚年龄人口
某研究将行走模式分为两类:一类是零星地短时间行走,另一类是不间断地行走10分钟以上。该研究追踪了某国16732名66岁至78岁女性,4年随访期间有804名女性去世。结果发现,不管是零星散步还是较长时间的不间断行走,步数更多的人寿命更长;在约4500步之后,这种效应趋于稳定。研究者提出,只要开始走路,就能降低老年女性死亡风险。
以下各项如果为真,哪项不能质疑研究者的结论?
中青年女性的生活方式和老年女性有很大不同,每天行走步数与死亡率没有显著关联
正确的走路方式,才能使身体变得健壮,不当的走路方式和姿势,会危害身体健康
在这个年龄段,每天能够自主行走达到一定步数,通常意味着有更好的整体健康状况
能够坚持走路的人,或者有更多的生活内容,或者有更好的健康意识,这两者均有益健康
在春运高峰时,某客运中心售票大厅站满等待买票的旅客,为保证售票大厅的旅客安全,大厅入口处旅客排队以等速度进入大厅按次序等待买票,买好票的旅客及时离开大厅。按照这种安排,如果开出10个售票窗口,5小时可使大厅内所有旅客买到票;如果开12个售票窗口,3小时可使大厅内所有旅客买到票,假设每个窗口售票速度相同。由于售票大厅入口处旅客速度增加到原速度的1.5倍,在2小时内使大厅中所有旅客买到票,按这样的安排至少应开售票窗口数为( )。
15
16
18
19
六朝时的清谈名家刘惔话很多,但他也欣赏不说话的人。他见江权不常开口,非常欢喜,说:“江权不会说话,而能够不说,真叫人佩服。”江权知道自己不善言谈,但他懂得藏拙。不是每个人都知道自己的缺点在什么地方,好为人师夸夸其谈者不计其数。能说话而爱说,情有可原;很多人明明不大会说话,偏偏说个不停,自曝其短,往往令人生厌。因此可以说,江权这样做,其实是一种极难得的聪明。
以下哪项如果为真,最能支持上述结论:
能言而能不言是一种极难得的聪明
不能言而能不言是一种自知的聪明
不能言而言其实是一种浮夸之举
不能言而不言其实是一种无奈之举
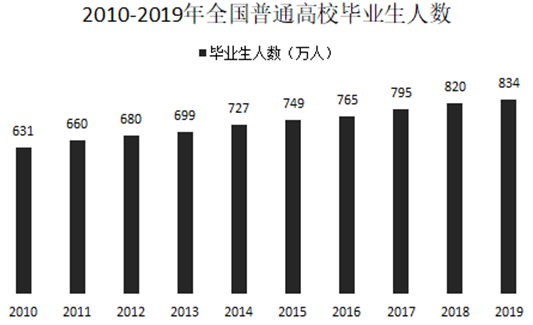
1979年全国普通高校毕业生人数为8.5万人,1980年为14.7万人,2001年为114万人,2002年为145万人,2010年较上一年同比增长3.4%,2018年首次突破了800万人,2019年预计达到834万人,毕业生就业创业面临严峻形势。
根据以上资料,下列说法正确的有:
①2019年全国普通高校毕业生人数约为1979年人数的100倍
②近5年全国普通高校毕业生人数基数很大,增长速率比较稳定,每年都是按照2%~5%的速度在增长
③近8年间累计培养全国普通高校毕业生人数已经超过6000万人,按现有的增长速度,估计2020年全国普通高校毕业生人数将达到840万人以上
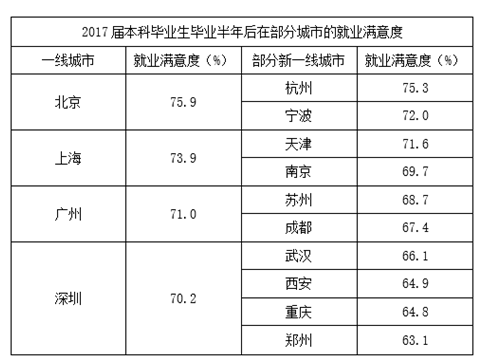
④2017届本科毕业生毕业半年后在各城市的就业满意度高于71%的城市有6个
⑤在一线城市中,北京是就业满意度最高的城市,其次是杭州
1个
2个
3个
4个
中世纪数学家比萨的莱奥纳多发现了斐波那契数列,它是这样一组数列:1、1、2、3、5······即后一数字为前面两个数字之和。那么,数列和树木的成长有什么关联呢?由于新生的枝条,往往需要一段“休息”时间,供自身生长,而后才能萌发新枝。所以,一株树苗在一段间隔,例如一年,以后长出一条新枝;第二年新枝“休息”,老枝依旧萌发;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则次年“休息”。这样,一株树木各个年份的枝桠数,便构成斐波那契数列。
这段文字意在说明:
斐波那契数列表现为树木的年轮增长
斐波那契数列在自然界中无处不在
斐波那契数列在自然中的应用
斐波那契数列表明植物在大自然中长期适应和进化
有一种理论认为,距今约5000万年前,生活在马达加斯加岛上的环尾狐猴、狐蝠以及其他哺乳动物的祖先当年乘坐天然的“木筏”,来到了马达加斯加这座位于印度洋的岛屿上。根据这一理论,来自非洲大陆东南部的哺乳动物当年漂流到马达加斯加,它们利用的交通工具是大原木或者漂浮的植被。在上演漂流记前,风暴将它们卷入大海,在洋流的带动下,这些古代“难民”漂流数周,来到马达加斯加。
以下哪项如果为真,不能支持上述漂流理论:
5000万年前,两个大陆板块周围的洋流曾一度向东流动,也就是流向马达加斯加
小型哺乳动物天生新陈代谢缓慢,能够在没有太多食物和淡水的情况下存活数周
在从非洲大陆东南部到达马达加斯加的动物中,没有大象,狮子等超重超大哺乳动物
5000万年前,非洲大陆和马达加斯加之间的距离与今天不同
素数是指只含有两个因子的自然数(即只能被自身和1整除),孪生素数是指两个相差为2的素数。比如,3和5,17和19等。所谓的孪生素数猜想,是由希腊数学家欧几里得提出的,意思是存在着无穷对孪生素数。该论题一直未得到证明。近期,美国一位华人讲师的最新研究表明,虽然还无法证明存在无穷多个之差为2的素数对,但存在无数多个之差小于7000万的素数对。有关方面认为,如果这个结果成立,那么将是数论发展的一项重大突破。
以下哪项如果为真,最能支持有关方面的观点:
7000万这个数字很大,离孪生素数猜想给出的2还有很大距离
这是第一次有人正式证明存在无穷多组间距小于定值的素数对
关于孪生素数猜想的证明需要一个漫长的、逐步推进的过程
这位华人讲师长期从事数学领域的相关教学和科研工作

 陕公网安备 61010302000399号
陕公网安备 61010302000399号