下列情景不可能发生在19世纪的是:
杰克打电话约玛丽一起去看电影
史蒂芬逊乘火车到斯托克顿旅行
约翰乘电梯登大楼楼顶拍照留念
汤姆通过广播收听葛底斯堡演说
3,5,8,11,16,19,( )
20
22
24
26
教育与产业毕竟有不同的利益诉求,双方是否能够采取产教融合的共同行动?有学者认为,德国的传统中小企业中存在大量的非研发创新或低技术创新的需求,正是这类创新,而不是大企业的技术研发,确保了德国制造业的长盛不衰。中国的中小企业数量远远多于德国,其技术能力远远落后于大企业,有大量的非研发创新或低技术创新的需求。这正是职业教育可以发挥作用的空间。
这段文字意在强调:
职业教育实施产教融合是可能与可行的
中小企业要注重学习德国既有的成功经验
职业教育需要强化服务中小企业的意识
中小企业要关注非研发创新与低技术创新
一家艺术馆馆藏了6幅18世纪画家的绘画作品,这些绘画作品按其价值由低到高排列如下:F、G、H、S、T和U。绘画作品F、G和H是风景画,而S、T和U是人物肖像画,每次这6幅作品中只能有3幅作品展出并需满足以下要求:
①展出的作品不能全部是风景画;
②如果展出的作品中只有一幅人物肖像画,则这幅人物肖像画必须是作品U;
③任何时候,H和T不能同时展出。
下列哪两幅作品如果被选中展出,则第三幅作品的选择面最广:
F和G
S和U
H和U
S和T
4,8,13,19,23,( ),34
25
27
28
31
-1,1,5,11,19,29,( )
30
31
32
41
2,4,6,9,13,19,( )
28
29
30
31
1,2,7,19,138,( )
2146
2627
3092
3865
在大学里讲美学,我不太会用到“竞争力”。美可能是一朵花,很难去想象如果我凝视这朵花,跟竞争力有什么关系。
我曾在美索不达米亚发现八千年前的一个雕刻:一个女孩子从地上捡起一朵落花闻。这个季节走过北京,如果地上有一朵落花,很可能一个北京的女孩子,也会把它拣起来闻。这是一个美的动作,它不是今天才发生的,八千年前的艺术品里就有。所以我在大学上美学课不谈竞争力,就谈这朵花。
那时,我在台湾中部的东海大学。校园很大,整个大度山都是它的校园,校园里到处都是花,每年四月开到满眼缭乱。教室的窗户打开,学生们根本不听我讲课。刚开始我有一点生气,可是我想,要讲美,我所有的语言加起来其实也比不上一朵花。所以我就做了一个决定:“你们既然没办法专心听课,我们就去外面。”他们全体欢呼,坐在花树底下,我问:“为什么你觉得花美?”有说形状美,有说色彩美,有说花有香味……
把这一切加起来,我们赫然发现:花是一种竞争力。它的美其实是一个计谋,用来招蜂引蝶,背后其实是延续生命的旺盛愿望。植物学家告诉我,花的美是在上亿年的竞争中形成的,不美的都被淘汰了。为什么白色的花香味通常都特别浓郁,因为它没有色彩去招蜂引蝶,只能靠嗅觉。我们经常赞叹花香花美,“香”和“美”这些看起来可有可无的字,背后隐藏着生存的艰难。
后来我跟学生做一个实验,我们用布把眼睛蒙起来,用嗅觉判断哪是含笑,哪是百合,哪是栀子,哪是玉兰……这个练习告诉我们,具体描述某一株花“香”是没有意义的,每种花的香味都不一样,含笑带一点甜香,茉莉的香气淡远……美是什么?另一种物种没法取代才构成美的条件。我问学植物的朋友:“如果含笑的香味和百合一样会怎样?”他说:“那它会被淘汰了,因为它东施效颦,没有找到自己存在的理由。”所以我常常给美下一个定义:美是回来做自己。
关于“美是回来做自己”,最符合短文原意的一项是:
人需要自我观照
美是生物生存的需要
一个美的动作可以跨越千年
凸显个性的需求
我和我在基础物理学界的同事们是爱因斯坦的理性的后继者,乐于自认为我们是在探求美。有些物理方程丑得让人不愿多看一眼,更不用说把它们写下来了。毫无疑问,终极设计者只会用美的方程来设计这个宇宙!我们宣称,如果有两个都可用来描述自然的方程,我们总要选择能激起我们的审美感受的那一个。“让我们先来关心美吧,真用不着我们操心!”这就是基础物理学家们的呼声。
读者也许会把物理看成一个具有精确预言性而不适于审美沉思的科学。其实,审美事实上已经成了当代物理学的驱动力。物理学家已经发现了某些奇妙的东西:大自然在最基础的水平上是按美来设计的。我希望与你们分享的正是这种奇妙的感受。
“美”一词被赋予了一定的内涵。在日常生活中,我们对美的感受是依赖于心理、文化、社会甚至常常是生理等因素的。物理学显然不会关心这一类的美。
自然在她的定律中向物理学家展示的美是一种设计美。因强调几何对称,这种美在一定程度上使我们想到了古典建筑。物理学家在审视自然时所用的美学体系也是从这种朴素的几何确定性中吸取精髓的。请在纸上画出一个圆、一个正方形和一个矩形。快,哪一个图形更能使你愉悦?按古希腊人的观点,多数人大概会选择圆。当然,正方形甚至矩形也不会没有热忱的崇拜者。但存在一个客观的判据,它按圆形、正方形、矩形的次序来排定三种图形的名次,按此次序:圆具有更高的对称性。
或许我不该问哪一个图形更美,而该问哪一个图形的对称性更高。但是,按古希腊人对球形以及它们所构成的天体的完美性的雄辩论述,我还是要继续将对称等同于美。
对称性的精确数学定义涉及到不变性的概念。如果一个几何图形在某些操作下保持不变,就说这个图形在这些操作之下具有不变性。例如,圆在绕它的中心旋转时是不变的。作为一个抽象实体,不管我们把它转17度还是转其它角度,这个圆都不会变。而正方形就不一样,只有绕它的中心转90°、180°、270°和360°时(考虑对几何图形的影响时,转360°和转0°或不转是等价的)才保持不变。矩形的对称性比正方形的还要低,只有绕它的中心转180°和360°时才保持不变。
按原文的意思,作者将对称等同于美是因为:
圆在绕它的中心旋转时是不变的
圆具有更高的对称性
按古希腊人对球形以及它们所构成的天体的完美性的雄辩论述
对称性图形更能让人愉悦



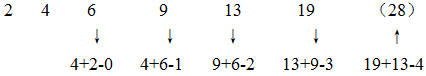
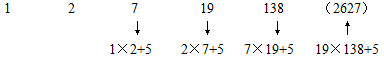
 陕公网安备 61010302000399号
陕公网安备 61010302000399号