一项足球比赛共有8支队伍参加,每两支队伍之间需要踢两场比赛,获胜得3分,打平得1分,落败不得分。在该项足球比赛中,获得第一名的队伍积分最多可能比第二名多( )分。
40
30
20
10
某工厂有100名工人报名参加了4项专业技能课程中的一项或多项。已知A课程和B课程不能同时报名,如果按照报名参加的课程对工人进行分组,将报名参加的课程完全一样的工人分到同一组中,则人数最多的组最少有多少人:
5
6
7
8
9
10
11
12
有30名学生,参加一次满分为100分的考试,已知该次考试的平均分是85分,问不及格(小于60分)的学生最多有几人:
9人
10人
11人
12人
某招考职位规定:凡通过英语专业八级、参加过支教活动的英语专业应届毕业生均有资格报考该职位。张华是北京某名牌大学英语专业的一名应届毕业生,却没有资格报考该职位。
由此一定可以推出的是:
张华没有通过英语专业八级考试
张华没参加过支教活动
如果张华通过了英语专业八级考试,那么他没有参加过支教活动
如果张华参加过支教活动,那么他通过了英语专业八级考试
为加强机关文化建设,某市直属机关在系统内举办演讲比赛,3个部门分别派出3、2、4名选手参加比赛,要求每个部门的参赛选手比赛顺序必须相连,问不同参赛顺序的种数在以下哪个范围之内:
小于1000
1000~5000
5001~20000
大于20000
甲和乙两个办公室分别选出2人听一个讲座。如每个办公室均随机选择,则甲办公室员工小刘和小陈同时被选中的概率正好为10%。乙办公室员工小吴被选中的概率为20%,则两个办公室共有多少名员工?
11
15
16
20
将0、2、4、6、8、1、3、5、7、9十个数字按顺时针方向排成环形,从其中的任一数字开始按顺时针方向连续取三个数形成的所有三位数的和为:
4983
4971
4995
无法确定
某次招标活动中,甲、乙、丙、丁、戊和己6家投标企业依次对自己的设计进行讲解。已知甲和乙均不能安排在第一个或最后一个,丙只能安排在第三个或第四个,如在满足以上条件的次序中随机选择一个,则丁和戊的讲解次序相邻的概率为:
2/9
1/5
2/7
1/4
某高校为加强对学生综合素质的培养,增设创新学分。学生参加社会服务表现积极和参与学术活动均可以获得创新学分。机电工程专业的学生都参与了学术活动。大多数机电工程专业的学生参加社会服务的时间都超过了80小时,其余学生参加社会服务的时间均不足60小时。参加社会服务时间达到60小时以上被认为表现积极,同时还可以获得优秀社会实践奖。
由此可以推出:
所有参与学术活动的机电工程专业学生都参加了社会服务
与其他专业的学生相比,获得创新学分的机电工程专业的学生更多
有些获得优秀社会实践奖的机电工程专业学生获得了创新学分
除参加社会服务时间达到60小时以上外,没有其他途径可以获得优秀社会实践奖
有一排长椅总共有65个座位,其中已经有些座位上有人就坐。现在又有一人准备找一个位置就坐,但是此人发现,无论怎么选择座位,都会与已经就坐的人相邻。问原来至少已经有多少人就坐:
13
17
22
33

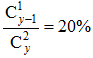 ,整理后得
,整理后得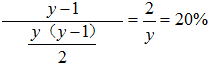 ,解得y=10,即乙办公室共有10人。
,解得y=10,即乙办公室共有10人。 陕公网安备 61010302000399号
陕公网安备 61010302000399号