周末，甲、乙、丙、丁在商场偶遇，一阵寒暄过后得知，他们几人在商场要么只看了电影，要么只购了物。
①丁有购物；
②如果甲有购物，那么乙去看了电影；
③如果丁没有购物，那么丙去看了电影；
④甲和乙都有购物。
如果以上陈述只有一项为真，可以推出：（ ）。
乙有购物，甲看了电影
丙有购物，乙看了电影
丙有购物，丁看了电影
甲和乙都看了电影
某单位准备从甲、乙、丙、丁、戊、已六人中择优录取数名技术人员，录用情况符合如下条件：
（1）丙和丁恰有一人被录取；
（2）甲和乙至少有一人被录取；
（3）甲和丁恰有一人被录取；
（4）录取乙当且仅当录用丙；
（5）甲、戊、己中恰有两人被录用。
根据上述信息，可以推出最终录用的人数为：（ ）。
2
3
4
5
一个工程的实施有甲、乙、丙和丁四个工程队供选择。已知甲、乙、丙的效率比为5：4：3，如果由丁单独实施，比由甲单独实施用时长4天，比由乙单独实施用时短5天。问四个队共同实施，多少天可以完成（不足1天的部分算1天）？
10
11
12
13
已知一次英语考试甲、乙、丙、丁的成绩如下：
甲、乙的成绩之和等于丁、丙的成绩之和，如果把乙和丁的成绩互换，甲和丁的成绩之和大于乙和丙的成绩之和，乙的成绩比甲、丙的成绩都高。
根据以上所知，下列哪项为真：
甲的成绩最高
乙的成绩最高
丙的成绩最高
丁的成绩最高
甲、乙、丙、丁、戊、己六位运动员的跳高纪录有如下比较：
(1)乙的成绩比丙好，但不如甲；
(2)丁的成绩不如甲和丙；
(3)戊的成绩好于丁和己，但不如甲和丙。
由此，可以确定：
丁的成绩好于己
己的成绩好于丁
戊的成绩好于乙
乙的成绩好于戊
M市年终机关作风评议工作即将开始，6位专家对市政府甲、乙、丙、丁、戊等5个重要部门分别作出如下预测：
（1）如果甲不能得第一，则丙一定会得第三；
（2）如果乙能得第二，则丁一定会得第四；
（3）如果甲得第一或者乙得第二，则丙一定会得第三；
（4）如果甲得第一，则乙得第二；
（5）丙不会得第三，而甲得第一和乙得第二都是有可能的；
（6）丙不会得第三，但戊会得第五。
评议结束后发现，6位专家中只有一位专家的话不符合评议结果。
据此，可以推出：
甲得第一
乙没有得第二
丙得第三
丁没有得第四
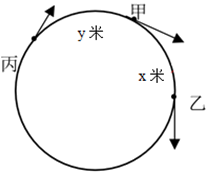
甲、乙、丙从长360米的圆形跑道上的不同点同时出发，沿顺时针方向匀速跑步。3分钟后甲追上乙，又过1分30秒后丙也追上乙，又过3分30秒后丙追上甲，又过5分30秒后丙第二次追上乙。问出发时甲在乙身后多少米？
48
84
108
144
米/分钟；
，用时为3+1.5+3.5=8分钟；
，
；
米/分钟，甲乙距离x=28×3=84米。扶贫干部某日需要走访村内6个贫困户甲、乙、丙、丁、戊和己。已知甲和乙的走访次序要相邻，丙要在丁之前走访，戊要在丙之前走访，己只能在第一个或最后一个走访。问走访顺序有多少种不同的安排方式？
32
48
16
24
种方式；
种方式；
种方式。某城市有5个公园。甲、乙、丙、丁、戊，它们由南至北基本在一条直线上，同时：
(1)乙与丁相邻并且在丁的北边
(2)戊和甲相邻
(3)丙在乙的北边
根据以上线索，可以推断五个公园由北至南的顺序可以是：
甲，丙，戊，乙，丁
乙，丁，戊，甲，丙
丙，甲，戊，乙，丁
丙，丁，乙，甲，戊
有一件未留姓名的好人好事在某社区传开，甲乙丙丁四人有如下对话：
甲说：这件事肯定是乙、丙、丁中的一位做的。
乙说：我没有做这件事，好人好事是丙做的。
丙说：此事是甲和乙中的一位做的。
丁说：乙说的是事实。
经调查，证实这四人中有两人说的符合实际。由此推出：
是甲做的好事
是乙做的好事
是丙做的好事
是丁做的好事
陕公网安备 61010302000399号