有一列数,第一个数为8,第二个数为4,从第二个数起,它们的每个数都比它前后相邻的两数的和少5,从第一个数到第2003个数的和是:
10001
10000
10011
11000
某在线教育机构在网上推出了一个面向中小学生的直播课,这个直播课在试播时组织了很多中小学生和家长免费观看,获得了很高的评价,但是在正式播出后,在线收看的人数并不理想。下列选项最不能解释这一现象的是( )。
正式的直播课程需要付费观看
该直播课的正式播出时间不合理
该直播课为系列课程,共计开设10节
其他在线教育机构推出了许多同类型的直播课
苗苗有一堆草莓,乐乐也有一堆草莓。苗苗的草莓五个五个地数,最后剩两个,七个七个地数,最后还是剩两个;乐乐的草莓五个五个地数,最后剩四个,六个六个地数,最后剩三个。已知苗苗比乐乐多8个草莓,则苗苗的草莓数为:
37
62
72
77
87
92
102
107
(1)对于西方汉学家来说,若想解读《红楼梦》,不仅要了解作者的生平,还要迈过好几道难关,才能_______,领悟其独特的艺术魅力。
(2)文艺复兴时期的绝世天才达·芬奇,既是一位艺术家和哲学家,同时又是工程师、物理学家和生物学家,他在上述每个领域,都达到了他那个时代_______的成就。
填入划横线部分最恰当的一组是:
登高望远 登坛拜将
登堂入室 登坛拜将
登堂入室 登峰造极
登高望远 登峰造极
2021年6月,国务院公布了第五批国家级非物质文化遗产代表性项目名录,其中新疆有5项入选,包括伊宁市俄罗斯族巴扬艺术、塔城市俄罗斯族踢踏舞、( )、青河县姑娘追、( )。
①于田县维吾尔族曲棍球
②阿图什市柯尔克孜族约隆歌
③木垒县哈萨克族刺绣
④莎车县维吾尔达瓦孜杂技
①③
①④
②④
③④
某影像杂志社编辑在广大革命老区从事摄影创作多年。他说,老区人民在脱贫攻坚奔小康的伟大实践中所展现出的艰苦奋斗、开拓进取、奋发向上的精神风貌,时时刻刻感动和吸引着我,给我提供了不竭的工作动力、喷涌的艺术灵感和丰沛的创作资源。以上事例体现的马克思主义哲学道理是:
①实践出真知
②生有涯知无涯
③实践是认识的来源
④认识服务实践指导实践
①③
①④
①②③
②③④
买学区房和交择校费,本质上没有区别,都表明了教育资源配置依然不_______。
填入划横线部分最恰当的一项是:
平行
均衡
均匀
平均
巩固计算思维是每个教育阶段的重要目标。只有这样,学生的能力才能在前一个水平的基础上向上发展。计算思维有助于任何领域问题的解决。比如,把一个大问题分解为若干个小问题,通过推理设计小型实验的可行性路径,以及与他人共同设计问题的解决方案。在不同环境下采用这些策略,可以让学生明白计算思维远比计算机有用。
关于这段文字,以下理解准确的是:
培养计算思维是教育的重要内容
应当减少学生对计算机的依赖
任何领域问题的解决都有赖于计算思维
可以通过分阶段的方式培养计算思维
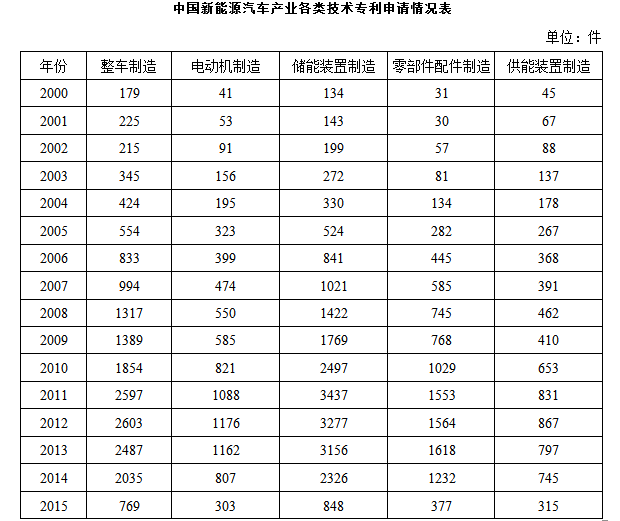
2001~2015年间,新能源汽车五种技术专利申请数均高于上年的年份有多少个:
7
8
9
10
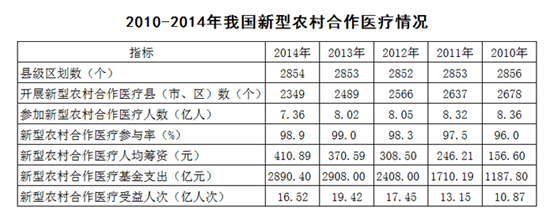
2010—2014年,开展新型农村合作医疗的县(市、区)数量占县级区划数90%以上的年份有()个:
1
2
3
4

 陕公网安备 61010302000399号
陕公网安备 61010302000399号