斑头雁在飞行中有一个特点,就是它们经常以某种队形来飞,通常是后面的鸟飞在前一只鸟的侧后方,因此就有了常见的“人”字形队形。一些研究者认为这一队形可减小空气阻力、降低飞行能耗,然而反对者认为如果是为了减小阻力,鸟更应该选择直线的队形,因为一个紧跟一个飞行能最大程度地减小跟随者需要克服的空气阻力。
以下哪项如果为真,最能质疑反对者的结论?( )
飞行过程中,领头雁会不时地与后方同伴换位,否则它们很容易精疲力尽
斑头雁飞行时偏移于前面的同伴,虽不能最大限度减小空气阻力,但能极大地减少上升时所需的体能消耗
斑头雁在飞行时会有确定方向的需求,所以并不会一直排成“人”字形飞行
速滑比赛中,运动员常以“人”字形前进,一名运动员在前,另外三名紧随其后,后三名队员因阻力变小而受益
①餐厅的客流量创历史新高
②开通外卖和网上团购业务
③入选当年大众点评必吃榜
④逐渐吸引更多的年轻顾客
⑤烤鸭老字号顾客群体断层
②④①③⑤
⑤②④③①
②①④③⑤
⑤③②④①
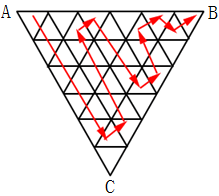
如图,某三角形展览馆由36个正三角形展室组成,每两个相邻展室(指有公共边的小三角形)都有门相通,若某参观者不愿意返回已参观过的展室(通过每个房间至多一次),那么他至多能参观多少个展室:
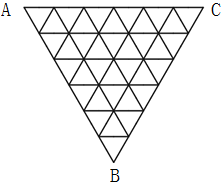
33
32
31
30
一位管理者让几位员工从皱纹纸带上各裁下一段30厘米的纸带,只能用目测,不能用量具测量。然后,又要求每一位听讲者裁150厘米和600厘米长的纸带各一段。大家裁完后,这位管理者掏出卷尺,仔细地测量一条条纸带并公布结果:30厘米一组,平均误差不到6%;150厘米一组,平均误差上升到11%;600厘米一组,平均误差高达19%,个别的相差100多厘米。
由此推出的是:
目标越小、越集中,越容易接近目标
目标越大、越宽泛,越不容易偏离目标
目标大小适中,最容易接近既定目标
目标大小与接近目标的程度无关
某训练基地的一块三角形场地的面积是1920平方米。已知该三角形场地的三边长度之比是5:12:13,则其周长是:
218米
240米
306米
360米
现有60枚1元硬币,若把它们在平面上紧密排列成正三角形,要使剩下的硬币尽可能少,则三角形的最大边长是:
11
10
8
6
平行四边形∶长方形∶正方形
点∶线段∶三角形
三角形∶等腰三角形∶等边三角形
线段∶三角形∶四边形
直线∶平面∶空间
公元前3世纪,古希腊数学家欧几里得提出:“三角形内角之和等于180度。”19世纪,德国数学家黎曼提出:“在球面上,三角形内角之和大于180度。”后来,俄国数学家罗巴切夫斯基又提出:“在凹面上,三角形内角之和小于180度。”这一认识过程说明:
真理具有绝对性
真理具有唯一性
真理具有客观性
真理具有相对性
如图所示,周长为24米的平行四边形绿化地被划分为三块区域,两边为三角形的花坛,中间为矩形的草地。已知a、b、c长度之比为4:2:![]() ,则矩形草地的面积为( )平方米。
,则矩形草地的面积为( )平方米。
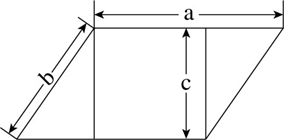
6
![]()
12
![]()
小王近期正在装修新房,他计划将长8米、宽6米的客厅按下图所示分别在各边中点连线形成的四边形内铺设不同花色的瓷砖,则需要为最里侧的四边形铺设多少平方米的瓷砖:

3
6
12
24



 陕公网安备 61010302000399号
陕公网安备 61010302000399号