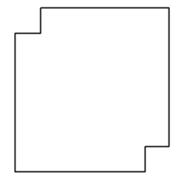
劳动技能课上老师给出一道手工题：一张正方形纸片，在一对对角处各减去一个边长为1厘米的小正方形（如下图所示），想办法把这个缺角的正方形恰好剪成一些长2厘米、宽1厘米的小矩形，问初始的大正方形边长要多大时，任务才有可能完成？
8
15
32
以上答案都不对
上海市城乡建设和交通发展研究院于2015年1月份发布《2014年上海综合交通运行年限》年报显示，2014年上海交通供需矛盾进一步突出，交通高峰时段延长，拥堵呈常态化。自2010年世博会以来，上海中心城区城市道路里程约4865公里，增长仅为3%；城市道路面积105平方公里，增长8%。而与之相对应的是私人小汽车数量的持续增长：截至2014年底，上海机动车保有量为304万辆左右（不含外省市号牌车辆），较2013年底增加20.5万辆，增幅为7.2%。数据显示，与2013年同期相比，2014年上海快速路日均交通总量增长约7%、中心城越江交通日均总量增长1.2%、高速公路日均车流总量增长约13.2%。
在机动车保有量迅速增长的同时，上海中心城区道路拥堵的累积时间延长，形成了早、午后、晚三个拥堵高峰、并逐步呈现午后高峰向晚高峰延伸，与晚高峰时段逐渐连成片以及早高峰提前的趋势。2014年，在42个快速路交通指数区域中，高峰时段拥堵指数大于50、累计拥堵时间大于1小时，超过100个工作日拥堵的有8个常发性严重拥堵区域，主要集中在浦西西部及西南面；在68个地面道路指数区域中有15个常发性严重拥堵区域，主要集中在内环内商圈及医院周边。
随着机动车数量的与日俱增，城市交通的承载压力越来越大，中心城区交通在一些时段和区域拥堵已成为司空见惯的现象，居民出行常常陷入苦不堪言的境地。各大城市也在不断探索治理拥堵的良方，其中“限购”是各地共同的做法，北京市从2014年到2017年，增量小客车指标额度供60万个。年度配置指标总量由24万个减少到15万个，从而使机动车保有量到2017年底不超过600万辆。2013年底，上海交通主管部门明确车牌价格调控措施将长期化，确定了全年总体10万张车牌的投放量。2014年天津市小客车指标投放量供10万个，按月分配，采取摇号和竞价的方式配置。2014年3月26日，杭州市政府规定杭州行政区域内小客车实行增量配额指标管理，增量指标须通过摇号或竞价方式取得。今后杭州每年汽车增量指标为8万个，按月度分配。
客观上，对小汽车进行“限购”，可以发挥的作用有：
有效解决城市拥堵的问题
直接限制小汽车的使用
有利于缓解因交通带来的环境污染
一定程度上促进公共交通的发展
一艘船往返于甲、乙两港口之间，已知水速为8千米/时，该船从甲到乙需要6小时，从乙返回甲需9小时，问甲、乙两港口的距离为多少千米：
216
256
288
196
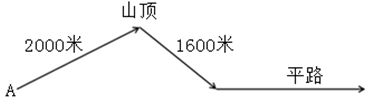
科研人员在山路测试救援机器人性能。已知救援机器人电池续航时间为60分钟，其上坡、下坡、平路速度分别为4米/秒、8米/秒、6米/秒。机器人从A点出发，沿箭头所示路线行进一定距离后折返，并在电量耗尽时正好返回A点。问机器人，在折返前最多能行进多少米？
6750
10350
13500
17100
秒；甲、乙、丙三员工共同修剪6060平方米草地，甲的修剪效率为30平方米/分钟，乙的修剪效率为40平方米/分钟，丙的效率为60平方米/分钟。上午，甲7点30分开始修剪，乙7点45分开始，丙8点15分开始，他们同一时间完成工作，乙用了( )分钟。
56
57
58
59
2016年8月16日我国发射了世界首颗量子科学实验卫星，这将使我国在世界上首次实现卫星和地面之间的量子通信。这颗卫星被命名为：
“孔子号”
“墨子号”
“孟子号”
“荀子号”
2021年6月11日，国家航天局公布了由祝融号火星车拍摄的着陆点全景、火星地形地貌、“中国印迹”和“着巡合影”等影像图。首批科学影像图的发布，标志着我国首次火星探测任务取得圆满成功。自祝融号2021年5月15日着陆火星开始，截至2022年5月1日，祝融号火星车累计行驶1921米，在火星表面工作342个火星日。
根据以上信息下列判断正确的是：
1个火星日比1个地球日略短
1个火星日比1个地球日略长
1个火星日与1个地球日的时长完全相等
1个火星年比1个地球年略短
在2008年8月8日至24日奥运会期间，北京市的空气质量不仅天天达标，而且有10天达到一级，全面兑现了对奥运会空气质量的承诺。下图是2008年1-8月北京市大气质量检测情况，图中一、二、三、四级是空气质量等级。一级空气质量最好，一级和二级都是质量达标天气。2008年北京的空气质量控制目标是全年达标天数累计达256天。
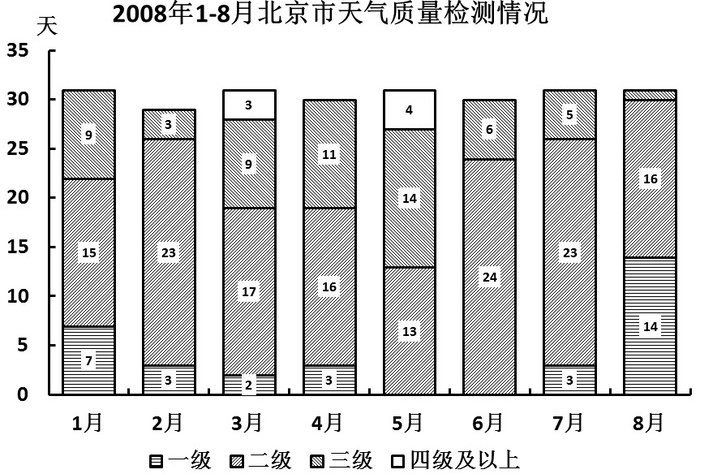
若将空气质量达标任务平均分配到各月，截至8月末，全年256天空气质量达标的计划完成情况是：
完成进度较慢
完成进度正常
完成进度提前
无法判断
一个长方形周长130厘米，如果它的宽增加
，长减少
，就得到一个相同周长的新长方形，则原长方形的面积为多少平方厘米：
1000
900
850
840
，化简得：
，又长方形的周长为130cm，则原长方形的长为40cm，宽为25cm，面积为40×25=1000。某工厂4个车间的工人都出生在1985到1988年间，如果统计任意2个车间的人数和，分别得到54、63、75、78、90、99这6个不同的结果。则人数最多的车间至少有多少工人出生于同一年：
14
15
16
17
陕公网安备 61010302000399号