某超市对甲和乙两种饮料进行特价促销,促销时间为周三到周六共4天。活动结束后发现,每天的饮料销售数量均为整箱,甲饮料每天的销售量为1到4箱不等,乙饮料每天的销售量为1至5箱不等,且销售量还符合以下规律:
①甲饮料每天销售的量并不相同,乙也如此。
②甲、乙销售数量总和随着日期推移每天增加1箱。
③星期三销售了3箱甲饮料,星期四销售了1箱甲饮料,星期六销售了5箱乙饮料。
由此可以推出:( )。
星期三甲、乙共销售了4箱
星期四甲、乙共销售了6箱
.星期五甲、乙共销售了8箱
星期六甲、乙共销售了10箱
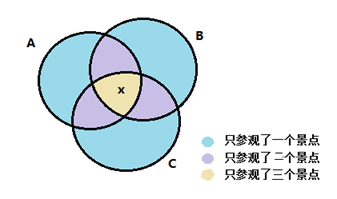
某旅行团共有48名游客,都报名参观了三个景点中的至少一个。其中,只参观了一个景点的人数与至少参观了两个景点的人数相同,是参观了三个景点的人数的4倍。则需要为这些游客购买多少张景点门票:
48
72
78
84
共有100个人参加某公司的招聘考试,考试内容共有5道题,1-5题分别有80人,92人,86人,78人和74人答对,答对了3道和3道以上的人员能通过考试,请问至少有多少人能通过考试:
30
55
70
74
3,3,4,5,7,7,11,9,( ),( )
13,11
16,121
18,11
17,13
一场超级篮球赛即将进入比赛最后阶段,4支球队将为最后名次展开激烈拼杀。行家们根据各球队以往战绩及现场表现,对比赛结果做出了3项预测:
(1)天空队、大地队都不能进入前两名;
(2)如果江河队获得第一,那么海洋队将获得第二;
(3)如果天空队获得第三,那么大地队将进入前两名。
比赛结束后,发现行家们预测只有一项是正确的。
据此,可以推出:
江河队获得第一
海洋队获得第二
天空队获得第三
大地队获得第四
某公司销售部拟派3名销售主管和6名销售人员前往3座城市进行市场调研,每座城市派销售主管1名,销售人员2名。那么,不同的人员派遣方案有:
540种
1080种
1620种
3240种
一次面试,试卷共有6道题。50个面试者回答后,答对的共有202人次。已知每人至少答对2题,答对2题的5人,答对4题的9人。答对3题和5题的人数同样多。则答对6题的人有几个:
5
6
7
8
胜利小学的225名同学与红旗小学的256名同学一起春游,将两所小学的同学混合在一起,随机组合,重新组织队伍,要求每队人数相同且队伍数尽可能少,那么胜利小学的张华与红旗小学的张明出现在同一队伍的概率约为( )
1.5%
2.5%
3.5%
4.5%
5.5%
6.5%
7.5%
8.5%
某次会议邀请4所高校每所各2位学者作报告。在某日上午、下午和晚上的三个时间段分别安排3位、3位和2位学者依次作报告,且同一所高校的2位学者不安排在同一时间段内作报告。问8人的报告次序有多少种不同的安排方式?
不到5000种
5000~10000种之间
10001~20000种之间
超过20000种
某单位要从甲、乙、丙、丁、戊、己6名工作人员中选派3名参加省职业技能大赛。有4位评委分别提出了自己的意见:
(1)甲、丙二人中至少选一人;
(2)乙、戊二人中至少选一人;
(3)乙、丙二人中至多选一人;
(4)甲、丁二人中至多选一人。
后来得知,戊因病不能参赛,并且上述4位评委的意见都得到了尊重。
根据上述信息,该单位选派的参赛选手是:
甲、乙、丙
甲、乙、丁
甲、乙、己
丙、丁、己

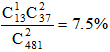 。
。 陕公网安备 61010302000399号
陕公网安备 61010302000399号